Предмет: Алгебра,
автор: Rorsherh
Как решаются такие уроавнения? Помогите!
Приложения:
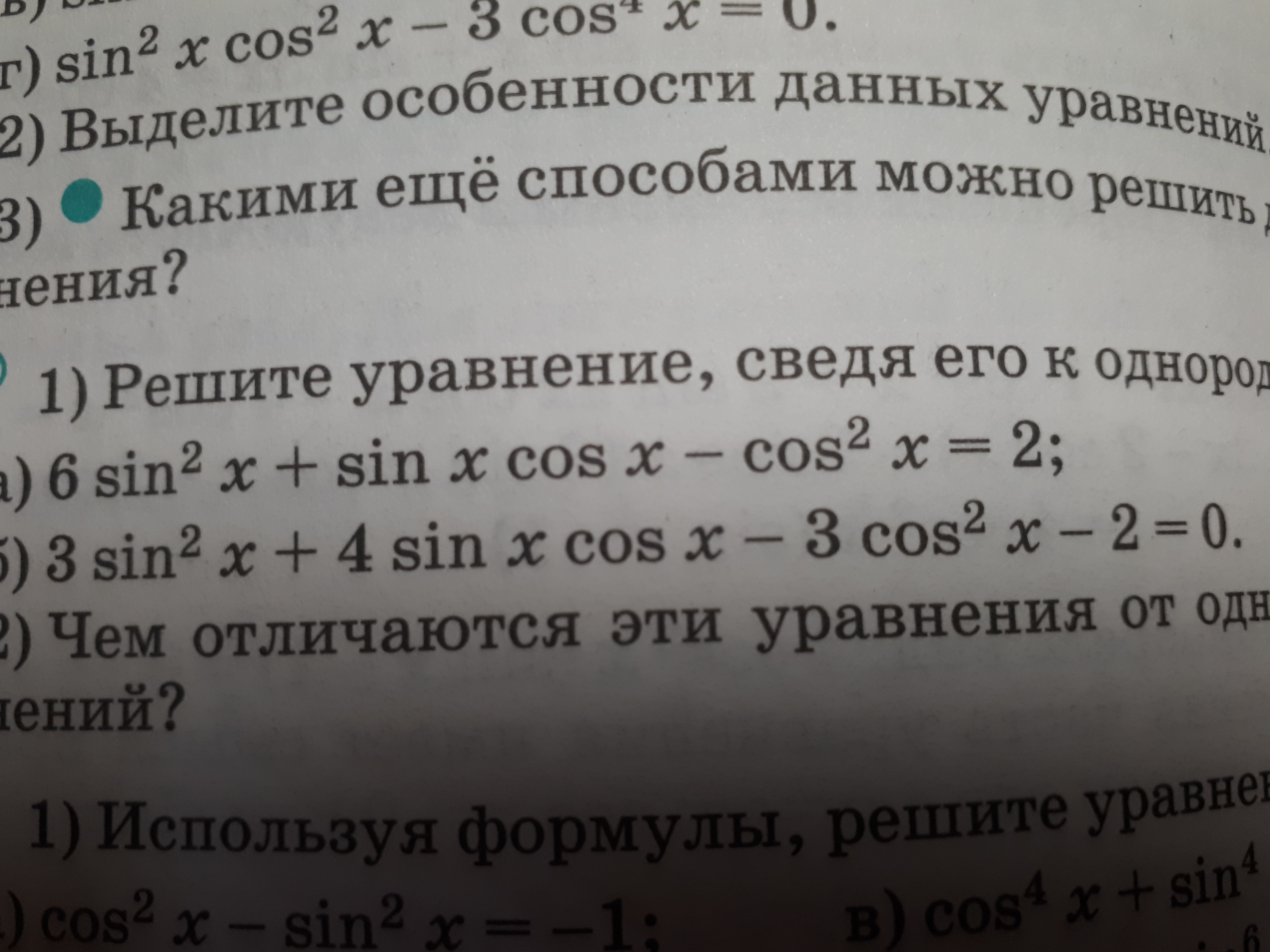
Ответы
Автор ответа:
1
во первых



Похожие вопросы
Предмет: Алгебра,
автор: alinysik15022008
Предмет: Қазақ тiлi,
автор: hhhsafia
Предмет: Химия,
автор: arinagrushko07
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: kama27041