Question

f(x)=-⅓x³+4x²-7x+18 найдите точки минимума и максимума

Answer 1

Ответ:

$\bf x_{max}=0 ~,~x_{min}=8$

Объяснение:

$\displaystyle \large f(x)=-\frac{1}{3}x ^3+4x^2-7x+18$

Найдём производную , для вычисления производных со степенями- воспользуемся с формулой $\bf (x^n)'=nx^{n-1}$

$\displaystyle \large f'(x)=3*(-\frac{1}{3}x )^2+2*4^1=0\\\large f'(x)=-x^2+8x=0\\\large -x^2+8x=0$

Решим уравнение . Если перед уравнением стоит отрицательный знак - то все знаки уравнения нужно поменять на противоположный.

$\large x^2-8x=0$

Вынесем x за скобки:

$\large x(x-8)=0\\\large x_1=0~~~~~~~~x-8=0\\\large~~~~~~~~~~~~~~~~x=0+8\\~~~~~~~~~~~~~~~~~\large x_2=8$

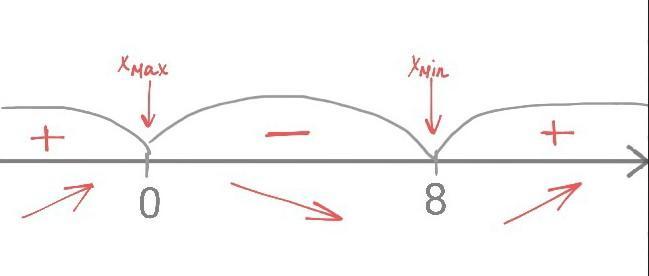
Найденные корни изобразим на числовой оси(см.фото) . Если знак производной меняется с плюса на минус - то это точка максимума , если знак производной меняется с минуса на плюс - то это точка минимума $\Rightarrow \bf x_{max}=0 ~,~x_{min}=8$