Предмет: Математика,
автор: 029уадцб1
на сторонах правильного треугольника АВС выбраны точки N M и L таким образом что NM перпендикулярен BC, ML перпендикулярен АВ и LN перпендикулярен АС. площадь треугольника АВС равна 36. чему равна площадь LMN?
Приложения:
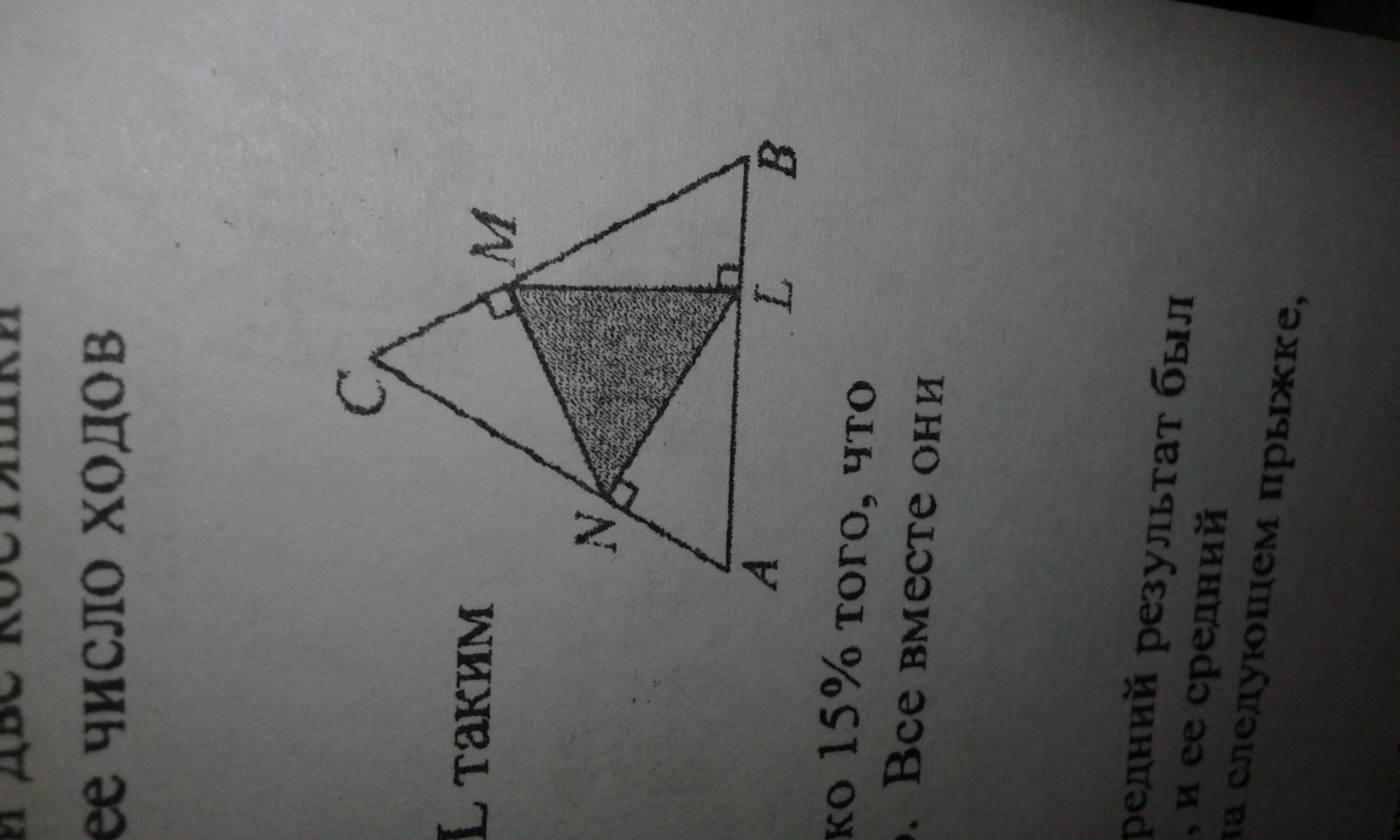
Kolde:
Варианты ответов есть?
да
вы отправьте я проверю
Ты чьо ни атветил, абищал жы
Ответы
Автор ответа:
3
Так как
треугольник правильный, то все его углы равны 60°.
Рассмотрим треугольник MLB. Угол LBM=60°, тогда угол BML=30°.
Пусть LB=х. Тогда MB=2х, так как катет, лежащий против угла в 30°, равен половине гипотенузы. По теореме Пифагора найдем ML:

Сторона исходного треугольника равна:

По построению, треугольник LMN правильный, значит он подобен с треугольником ABC.
Площади подобных треугольников относятся как квадрат коэффициента пропорциональности:

Ответ: 12
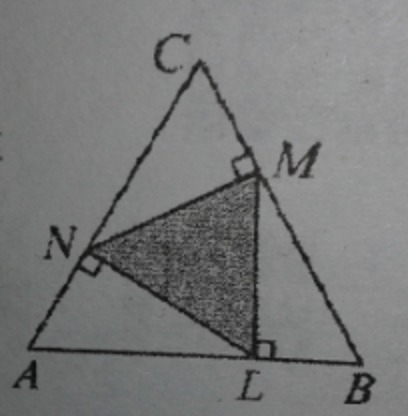
Рассмотрим треугольник MLB. Угол LBM=60°, тогда угол BML=30°.
Пусть LB=х. Тогда MB=2х, так как катет, лежащий против угла в 30°, равен половине гипотенузы. По теореме Пифагора найдем ML:
Сторона исходного треугольника равна:
По построению, треугольник LMN правильный, значит он подобен с треугольником ABC.
Площади подобных треугольников относятся как квадрат коэффициента пропорциональности:
Ответ: 12
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: evakobzeva33gmailcom
Предмет: Русский язык,
автор: tazhikovaardak4
Предмет: Литература,
автор: postrygang
Предмет: Литература,
автор: профф1