Предмет: Алгебра,
автор: Кариночка78
Помогите, пожалуйста, решить неравенство.
Приложения:
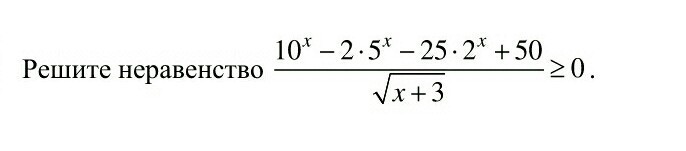
Ответы
Автор ответа:
0
При любых значениях х знаменатель положителен, значит знак дроби зависит от числителя:
Находим нули:
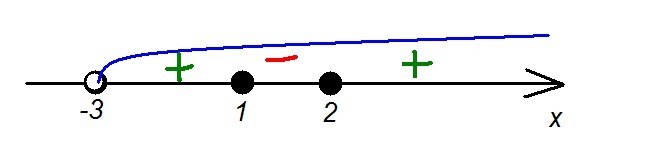
Отмечаем их на числовой прямой и применяем метод интервалов, учитывая условие
Ответ:
Приложения:
Похожие вопросы
Предмет: Литература,
автор: mellivell18
Предмет: Українська мова,
автор: nazarbutirin3
Предмет: Литература,
автор: 6qp2b258gf
Предмет: История,
автор: dashkaVip1
Предмет: Биология,
автор: Аноним