Предмет: Геометрия,
автор: eriklebdenko8
Срочно!! Пожалуйста помогите!
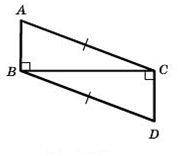
1) На рисунке АВ ⊥ ВС, CD ⊥ BC, AC = BD. Докажите, что АВ = CD.
2) Докажите равенство прямоугольных треугольников по катету и биссектрисе, проведенной из вершины прилежащего к этому катету острого угла.
3) Высоты АМ и СК треугольника АВС пересекаются в точке Н, НК = НМ. Докажите, то треугольник АВС равнобедренный.
Приложения:
eriklebdenko8:
Помогите пожалуйста)
Ответы
Автор ответа:
2
По равенству прямоугольных треугольников:
Треугольники равны по катету(т к общий) и гипотенузе(равны по условию)
2)АВ||CD (т к прямые углы при прямой ВС...)
АС||BD(т к углы при прямой ВС равны 90+х тоже ...)
Введем биссектрисы СК и ВМ
Катеты при биссектрисах равны =) ВС=ВС(общая)
Биссектрисы делят углы АСВ и СDВ пополам (х/2)
По подобию первых 2х строк СК||BM
СК=ВС*cos(x/2)
BM=BC*cos(x/2)
поэтому СК=ВМ
У треугольников равны катеты и биссектрисы(=следовательно и углы при них)
Треугольники равны
3)У равнобедренного треугольника должны быть равны АВ и ВС:
Можно соединить В и Н, тогда рассмотрим треугольники ВКН и ВМН
(=по гипотенузе и катету)
АКН и МСН подобны соответственно ВКН и ВМН в равных отношениях
значит АКН=МСН
Получаем ВК=ВМ, АК=МС (из равенств треугольников)
Складываем левые и правые части => АК+КВ=ВМ+МС
получаем АВ=ВС
это признак равнобедренного треугольника
АВС-равнобедренный
Треугольники равны по катету(т к общий) и гипотенузе(равны по условию)
2)АВ||CD (т к прямые углы при прямой ВС...)
АС||BD(т к углы при прямой ВС равны 90+х тоже ...)
Введем биссектрисы СК и ВМ
Катеты при биссектрисах равны =) ВС=ВС(общая)
Биссектрисы делят углы АСВ и СDВ пополам (х/2)
По подобию первых 2х строк СК||BM
СК=ВС*cos(x/2)
BM=BC*cos(x/2)
поэтому СК=ВМ
У треугольников равны катеты и биссектрисы(=следовательно и углы при них)
Треугольники равны
3)У равнобедренного треугольника должны быть равны АВ и ВС:
Можно соединить В и Н, тогда рассмотрим треугольники ВКН и ВМН
(=по гипотенузе и катету)
АКН и МСН подобны соответственно ВКН и ВМН в равных отношениях
значит АКН=МСН
Получаем ВК=ВМ, АК=МС (из равенств треугольников)
Складываем левые и правые части => АК+КВ=ВМ+МС
получаем АВ=ВС
это признак равнобедренного треугольника
АВС-равнобедренный
спасибо
https://znanija.com/task/28181979 не мог бы и тут чуток помочь???
Похожие вопросы
Предмет: Английский язык,
автор: veronikadalavurak
Предмет: Английский язык,
автор: veronikadalavurak
Предмет: Русский язык,
автор: agatavlyblennaya
Предмет: Химия,
автор: dashalg
Предмет: Литература,
автор: яяяяя1503