Предмет: Математика,
автор: Дмитрий1425
Сделать с полным объяснением ,не выходить за рамки 10 класса
Приложения:
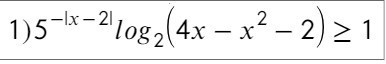
Ответы
Автор ответа:
1
можно оценить значения функций в обеих частях неравенства (на пять в степени... можно разделить обе части неравенства, т.к. это число всегда строго больше нуля и знак неравенства не изменится))
обе функции (и логарифмическая и показательная) имеют основание больше 1, следовательно с ростом аргумента будут возрастать...
на ОДЗ логарифм принимает любые значения: он от минус бесконечности возрастает до 1 при изменении аргумента от (2-√2) до вершины параболы в точке х=2, потом строго убывает...
а 5 в степени |x-2| наоборот, убывает для х∈(2-√2; 2)...
и "встречаются" эти функции только в точке х=2, т.е.
логарифм не бывает больше (график выше) показательной функции,
потому это неравенство выполняется только со знаком "="
Ответ: х=2
обе функции (и логарифмическая и показательная) имеют основание больше 1, следовательно с ростом аргумента будут возрастать...
на ОДЗ логарифм принимает любые значения: он от минус бесконечности возрастает до 1 при изменении аргумента от (2-√2) до вершины параболы в точке х=2, потом строго убывает...
а 5 в степени |x-2| наоборот, убывает для х∈(2-√2; 2)...
и "встречаются" эти функции только в точке х=2, т.е.
логарифм не бывает больше (график выше) показательной функции,
потому это неравенство выполняется только со знаком "="
Ответ: х=2
Приложения:
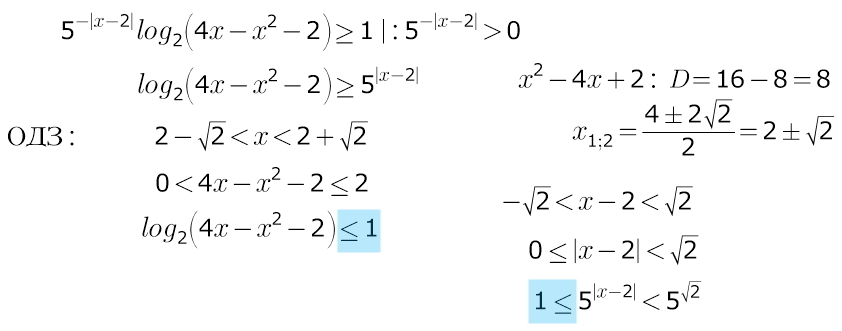
Аноним:
что-то мне непонятно почему в последней строке первого столбца логарифм <=1?
у вас же вышло что 5 в модуле >=1///
5 в степени я рассмотрела отдельно))
а логарифм ограничен в своих значениях областью определения...
значения функции (аргумент для логарифма) от 0 до 2 --строка выше... значит логарифм по основанию 2 принимает значения ДО 1
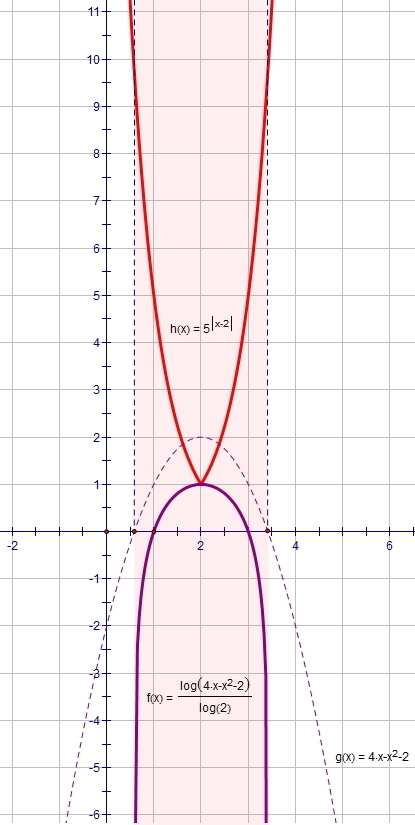
во втором файле график...
Похожие вопросы
Предмет: Алгебра,
автор: najmiddinovv
Предмет: Геометрия,
автор: dmytro007
Предмет: Математика,
автор: daria8mela
Предмет: Математика,
автор: натали242
Предмет: Математика,
автор: ппрн2