Предмет: Алгебра,
автор: 1231231241233
Решите уравнение:
log3(4x)+log3(9x)+log3(x)=log3(18x)+log3(3x)
Ответы
Автор ответа:
1
Решение в прикрепленном файле
Приложения:
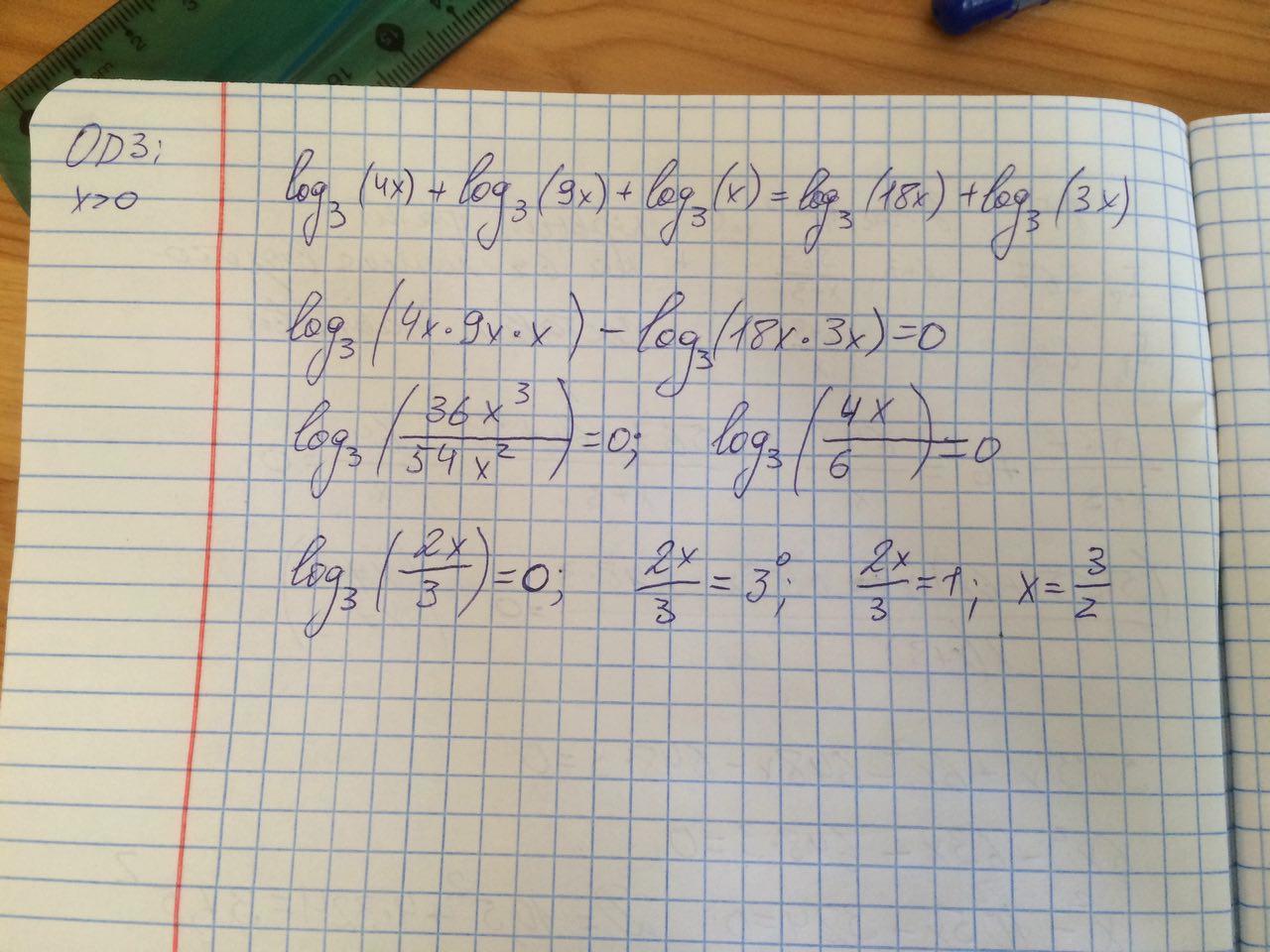
Автор ответа:
1
log₃(4x)+log₃(9x)+log₃x=log₃(18x)+log₃(3x) ОДЗ: x>0
log₃(4x*9x*x)=log₃(18x*3x)
log₃(36x³)=log₃(54x²)
log₃(54x³)-log₃(36x²)=0
log₃(54x³/36x²)=0
log₃(1,5x)=0
1,5x=3⁰
1,5x=1
3x/2=1
x=2/3
Ответ: х=2/3.
log₃(4x*9x*x)=log₃(18x*3x)
log₃(36x³)=log₃(54x²)
log₃(54x³)-log₃(36x²)=0
log₃(54x³/36x²)=0
log₃(1,5x)=0
1,5x=3⁰
1,5x=1
3x/2=1
x=2/3
Ответ: х=2/3.
Похожие вопросы
Предмет: Математика,
автор: kirakuz180611
Предмет: Геометрия,
автор: sasha444562
Предмет: Математика,
автор: togrulquliyev254
Предмет: География,
автор: баклажанчик228