Предмет: Геометрия,
автор: nervozz
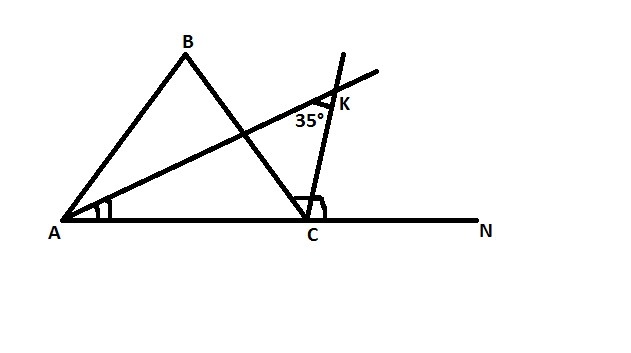
100 баллов! Биссектриса угла A треугольника ABC пересекает биссектрису внешнего угла при вершине C в точке K, угол AKC равен 35. Найти величину угла B.
Kазак:
70 градусов
Ответы
Автор ответа:
4
Назовём внешний угол при С - ∠BCN
По свойствам внешнего угла ∠BCN равен сумме не смежных с ним внутренних углов Δ-ка
∠BCN = ∠A + ∠B
Видно, что CK - биссектриса ⇒ ∠BCK = ∠KCN =
∠KCN = ∠KAC + ∠AKC
∠KAC =
∠KCN = ∠KAC + 35
 + 35° (·2)
+ 35° (·2)
∠A + ∠B = ∠A + 70°
∠B = 70°
По свойствам внешнего угла ∠BCN равен сумме не смежных с ним внутренних углов Δ-ка
∠BCN = ∠A + ∠B
Видно, что CK - биссектриса ⇒ ∠BCK = ∠KCN =
∠KCN = ∠KAC + ∠AKC
∠KAC =
∠KCN = ∠KAC + 35
∠A + ∠B = ∠A + 70°
∠B = 70°
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: A6N6D6R6E6W6
Предмет: Русский язык,
автор: viktoriaholland
Предмет: Литература,
автор: druzhininartur2010
Предмет: Математика,
автор: радима5