Предмет: Математика,
автор: lizka20011901
ОЧЕНЬ СРОЧНО (ТЕРМІНОВО)
БУДУ ОЧЕНЬ БЛАГОДАРНА ЗА РЕШЕНИЕ!
1) Дана функция:
y=3x3−4x4+10x2−−√5+12
Найти производную функции.
2) Дано:
1. u(x0)=−4 і u'(x0)=−2;
2. v(x0)=−3 і v'(x0)=−2;
3. f(x)=u(x)v(x)
Вычисли значения f'(x0)
3) Найти производную функции: y=6sinα+8ctgα−5arccosα.
а) y′=6cosα+8⋅1cos2α−5⋅αα2−1−−−−−√
б) y′=6cosα+8⋅1sin2α+5⋅11−α2−−−−−√
в) y′=−6⋅cosα−8⋅1sin2α+5⋅1α2−1−−−−−√
г) y′=6⋅cosα−8⋅1sin2α+5⋅11−α2−−−−−√
4) Напиши уравнение касательной к графику функции f(x)=x2+4x+3 в точке с абсциссой x0=1.
Приложения:



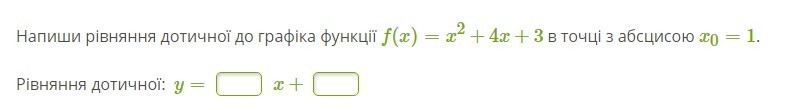
Ответы
Автор ответа:
2
1)
![y = 3{x}^{3} - \frac{4}{ {x}^{4} } +10 \sqrt[5]{ {x}^{2} } +12 \\ y' = 9 {x}^{2} + \frac{16}{ {x}^{5} } + \frac{4}{ \sqrt[5]{ {x}^{3} } } y = 3{x}^{3} - \frac{4}{ {x}^{4} } +10 \sqrt[5]{ {x}^{2} } +12 \\ y' = 9 {x}^{2} + \frac{16}{ {x}^{5} } + \frac{4}{ \sqrt[5]{ {x}^{3} } }](https://tex.z-dn.net/?f=y+%3D+3%7Bx%7D%5E%7B3%7D++-++%5Cfrac%7B4%7D%7B+%7Bx%7D%5E%7B4%7D+%7D+%2B10+%5Csqrt%5B5%5D%7B+%7Bx%7D%5E%7B2%7D+%7D+%2B12+%5C%5C+y%27+%3D+9+%7Bx%7D%5E%7B2%7D+++%2B+%5Cfrac%7B16%7D%7B+%7Bx%7D%5E%7B5%7D+%7D++%2B++%5Cfrac%7B4%7D%7B+%5Csqrt%5B5%5D%7B+%7Bx%7D%5E%7B3%7D+%7D+%7D+)
2)

u(x0)=−4 і u'(x0)=−2
v(x0)=−3 і v'(x0)=−2

3) Найти производную функции: y=6sinα+8ctgα−5arccosα.
ответ:
г)
4)

уравнение касательной:

2)
u(x0)=−4 і u'(x0)=−2
v(x0)=−3 і v'(x0)=−2
3) Найти производную функции: y=6sinα+8ctgα−5arccosα.
ответ:
г)
4)
уравнение касательной:
Похожие вопросы
Предмет: Алгебра,
автор: ZnanijaFrend
Предмет: Английский язык,
автор: neya2010
Предмет: Русский язык,
автор: 122333444460
Предмет: История,
автор: Александр876