Предмет: Математика,
автор: импрсарма
Помогите с решением интегралов,срочно
Приложения:
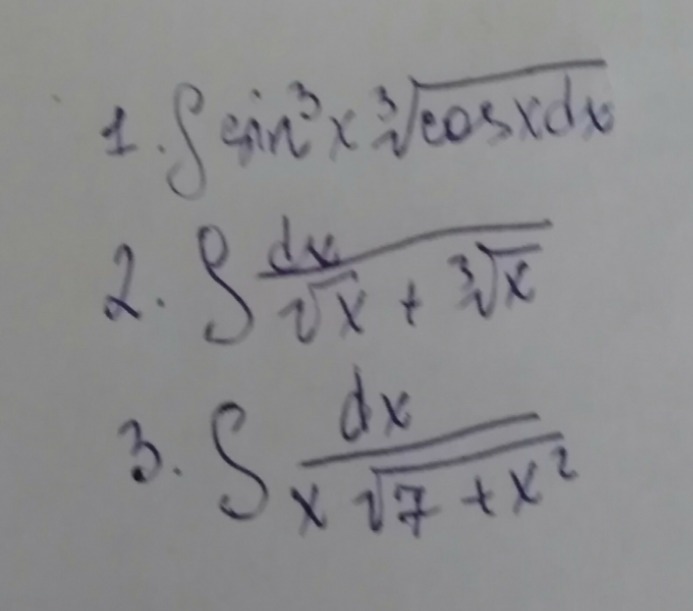
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Биология,
автор: valerijaosad4aja
Предмет: Обществознание,
автор: wrriwiaak
Предмет: Биология,
автор: savchenkomargarita09
Предмет: Алгебра,
автор: ILiveYou
Предмет: Алгебра,
автор: JJJJJOOOHH