Предмет: Алгебра,
автор: markovasabrina
Помогите пожалуйста решить тригонометрическое уравнение
Приложения:
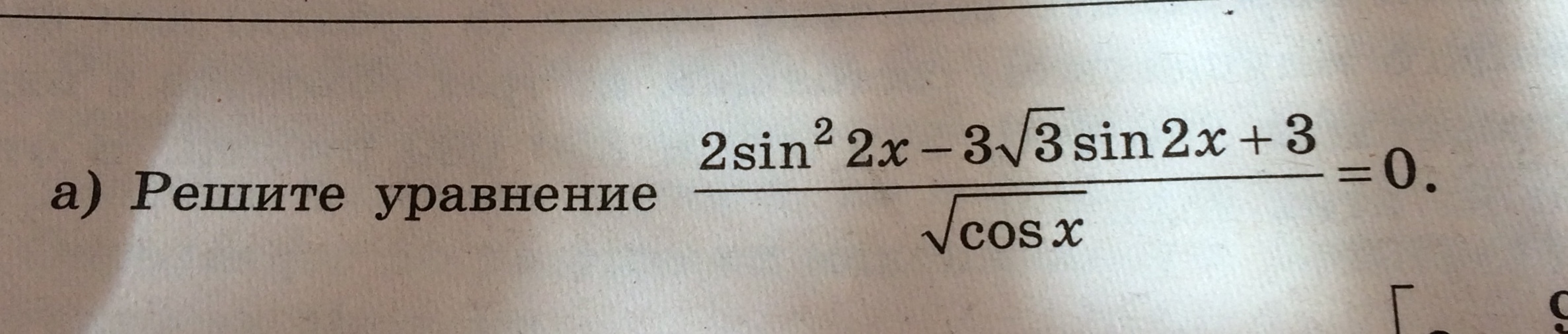
Ответы
Автор ответа:
0
2Sin² 2x -3√3Sin2x + 3 = 0
Cosx > 0
решаем эту систему:
Sin2x = t
2t² -3√3 t + 3 = 0
D = 27 -24 = 3
t₁ = (3√3 +√3)/4 = √3 t₂ = (3√3 -√3)/4=2√3/4 = √3/2
Sin2x = √3 Sin2x = √3/2
∅ 2x = (-1)^n π/3 + πn , n ∈Z
x = (-1)^n π/6 + πn/2 , n ∈ Z
Ответ: х = (-1)^n π/6 + (2n +1)π/2, n ∈Z
Cosx > 0
решаем эту систему:
Sin2x = t
2t² -3√3 t + 3 = 0
D = 27 -24 = 3
t₁ = (3√3 +√3)/4 = √3 t₂ = (3√3 -√3)/4=2√3/4 = √3/2
Sin2x = √3 Sin2x = √3/2
∅ 2x = (-1)^n π/3 + πn , n ∈Z
x = (-1)^n π/6 + πn/2 , n ∈ Z
Ответ: х = (-1)^n π/6 + (2n +1)π/2, n ∈Z
Похожие вопросы
Предмет: Українська мова,
автор: marixwz
Предмет: Алгебра,
автор: sansahaste
Предмет: Українська мова,
автор: torihaha3
Предмет: Математика,
автор: hjvhcgg
Предмет: Геометрия,
автор: narmin123