Предмет: Математика,
автор: NSjust
Помогите с решением интегралов, пожалуйста
Приложения:
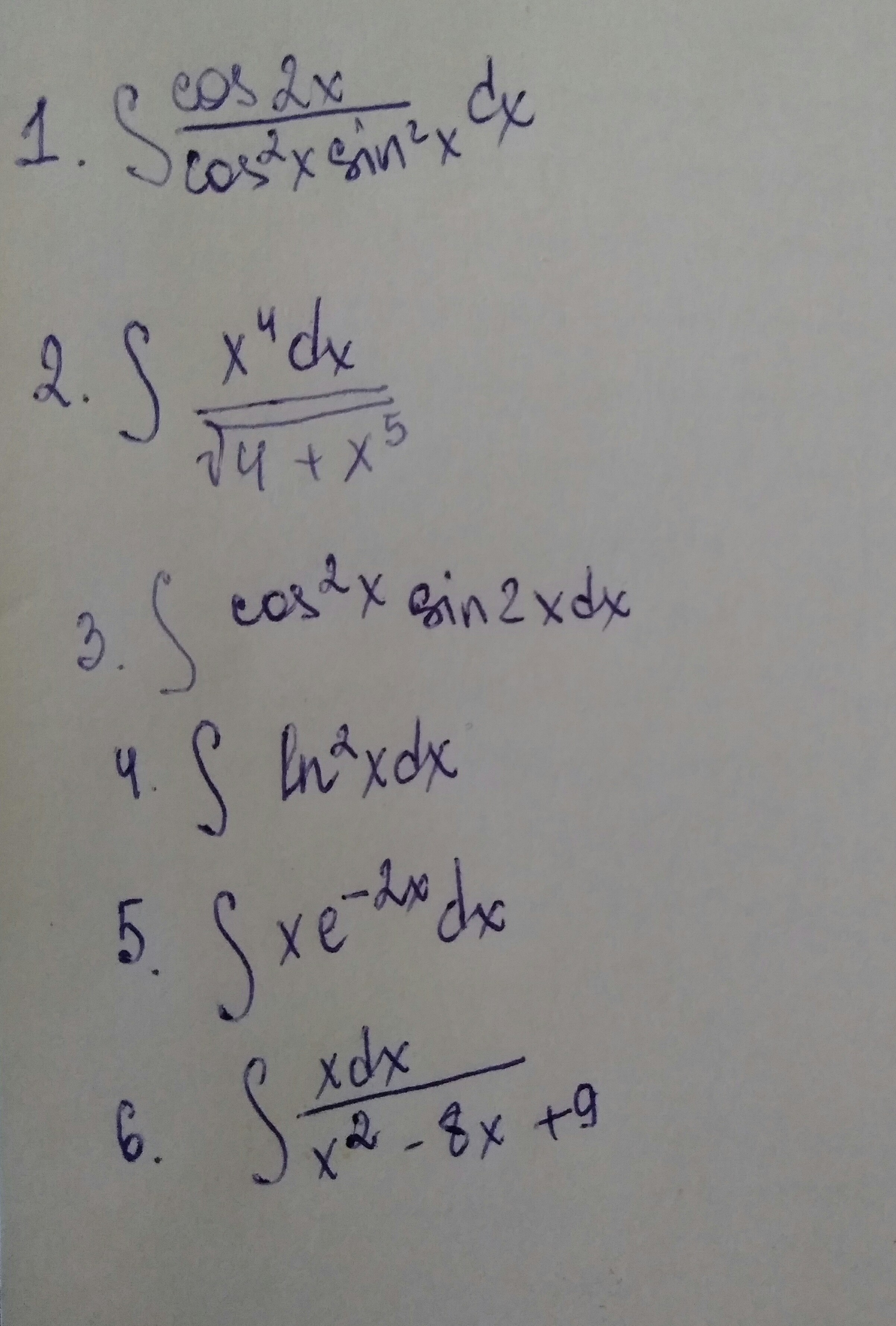
Ответы
Автор ответа:
1
импрсарма:
спасибо большое
Похожие вопросы
Предмет: Другие предметы,
автор: holynn
Предмет: Английский язык,
автор: sia1608
Предмет: Английский язык,
автор: kkarima0408
Предмет: Математика,
автор: еунига
Предмет: Обществознание,
автор: alfis99