Предмет: Алгебра,
автор: Vakluver
Самостоятельная работа по этой теме : Исследование и построение графиков функций с помощью производной
Решите пожалуйста
Приложения:
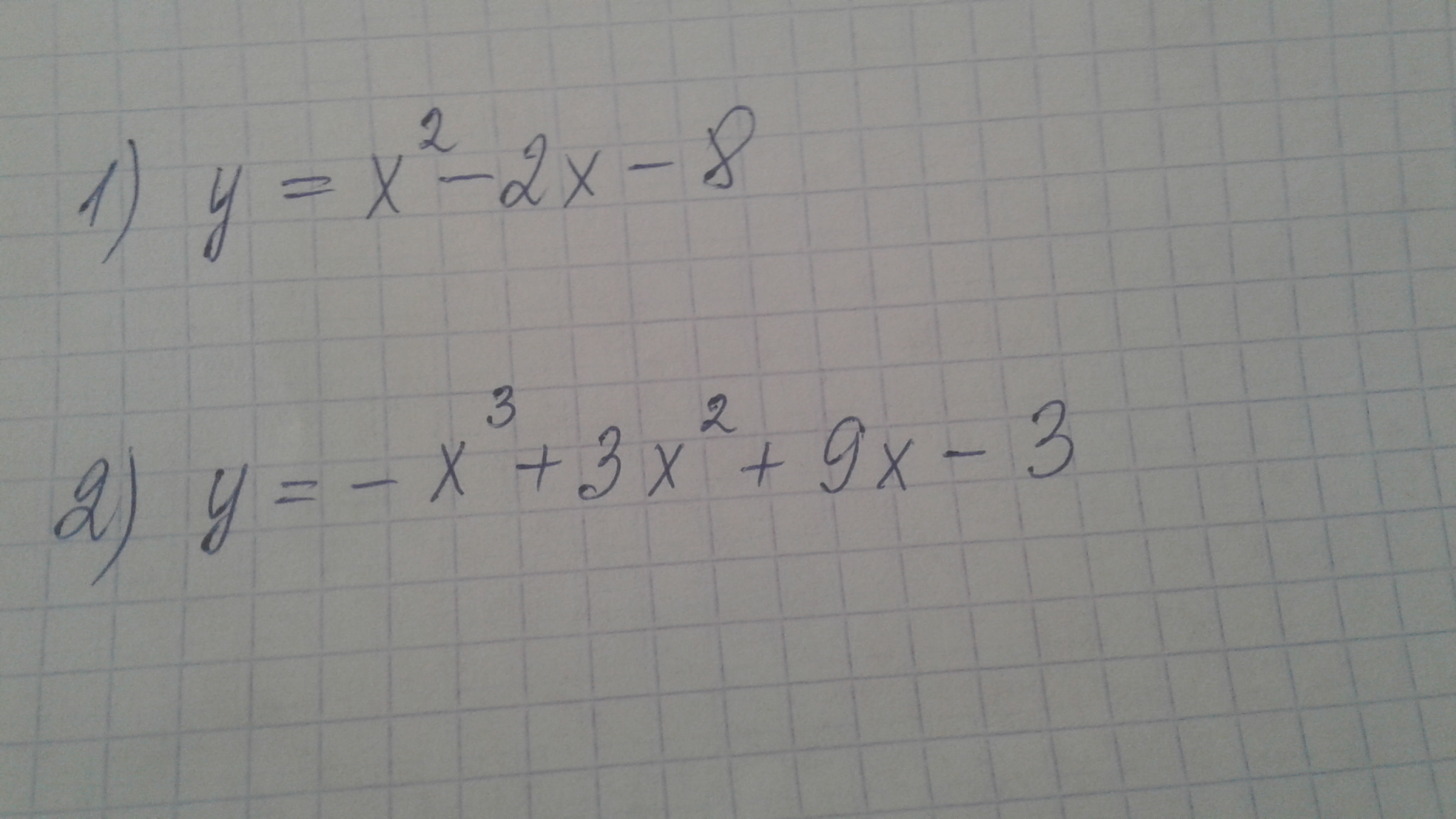
Ответы
Автор ответа:
1
1) y = x^2-2x-8 - парабола, ветви направлены вверх
Найдем вершину (x0;y0)
x0 = -b/2a = -(-2)/2*1 = 2/2=1
y0 = y(1) = -9
(1;-9) - вершина параболы
Найдем производную
y' = 2x-2
Найдем ее нули
2x-2=0
x = 1
При x < 1 y' < 0 => функция убывает на промежутке (-бесконечность;1)
При x > 1 y' > 0 => функция возрастает на промежутке (1;+бесконечность)
Дальше нужно доп.точки взять, к примеру, найти нули самой функции
y = x^2-2x-8 = 0
x1 = 4 ; x2 = -2
Осталось только график построить :)
2) y = -x^3+3x^2+9x-3
Найдем производную
y' = -3x^2+6x+9
Найдем ее нули
-3x^2+6x+9 = 0 | разделим на -3
x^2-2x-3=0
x1 = 3 ; x2= -1
Посмотрим, как ведет себя производная в районе этих точек
при x < -1 y' < 0 => y убывает на промежутке (-бесконечность;1)
при -1<x<3 y'> 0 => y возрастает на промежутке (-1;3)
при x > 3 y'<0 => y убывает на промежутке (3;+бесконечность);
Со 2 тоже в принципе, все, осталось только доп.точки взять и построить
Найдем вершину (x0;y0)
x0 = -b/2a = -(-2)/2*1 = 2/2=1
y0 = y(1) = -9
(1;-9) - вершина параболы
Найдем производную
y' = 2x-2
Найдем ее нули
2x-2=0
x = 1
При x < 1 y' < 0 => функция убывает на промежутке (-бесконечность;1)
При x > 1 y' > 0 => функция возрастает на промежутке (1;+бесконечность)
Дальше нужно доп.точки взять, к примеру, найти нули самой функции
y = x^2-2x-8 = 0
x1 = 4 ; x2 = -2
Осталось только график построить :)
2) y = -x^3+3x^2+9x-3
Найдем производную
y' = -3x^2+6x+9
Найдем ее нули
-3x^2+6x+9 = 0 | разделим на -3
x^2-2x-3=0
x1 = 3 ; x2= -1
Посмотрим, как ведет себя производная в районе этих точек
при x < -1 y' < 0 => y убывает на промежутке (-бесконечность;1)
при -1<x<3 y'> 0 => y возрастает на промежутке (-1;3)
при x > 3 y'<0 => y убывает на промежутке (3;+бесконечность);
Со 2 тоже в принципе, все, осталось только доп.точки взять и построить
Похожие вопросы
Предмет: Алгебра,
автор: serebryanskaya24
Предмет: Українська література,
автор: alechenkodima2007
Предмет: Қазақ тiлi,
автор: pyatiyx
Предмет: Математика,
автор: какоймеркой
Предмет: Математика,
автор: таол