Предмет: Математика,
автор: Infinity167
найдите число целых решений неравенства
Приложения:
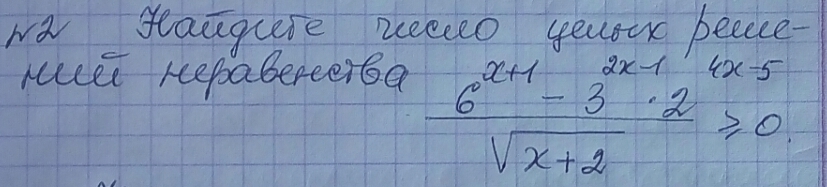
Ответы
Автор ответа:
3
Ответ: 4
Похожие вопросы
Предмет: Русский язык,
автор: elakim271
Предмет: Математика,
автор: comfypavl9020
Предмет: Биология,
автор: mariakvitko
Предмет: Математика,
автор: veronikatoirov
Предмет: Алгебра,
автор: nikolas2000