Предмет: Алгебра,
автор: etm692
30 баллов за решение.
Помогите решить эти 2 уравнения, подробно, желательно на листочке тетради.
8 КЛАСС
Приложения:
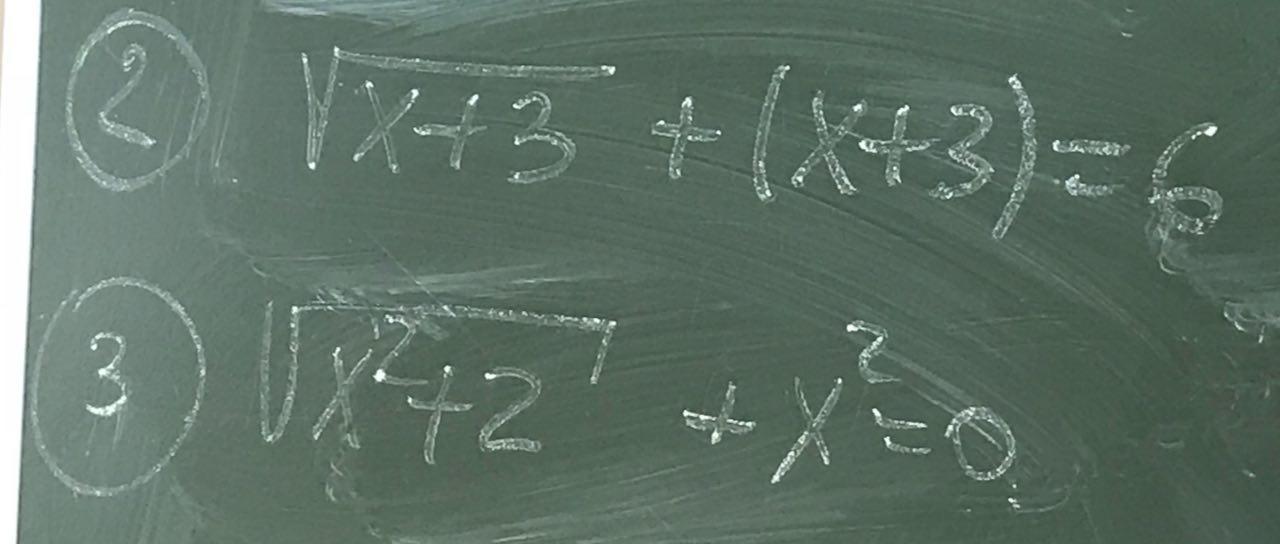
Ответы
Автор ответа:
1
2.  +х+3=6
+х+3=6
 =6-3-х
=6-3-х
 =3-х
=3-х
возводим в квадрат обе части уравнени
х+3=(3-х)^2
x+3=9-6x+
 -6х-х+9-3=0
-6х-х+9-3=0
 -7х+6=0
-7х+6=0
D-49-6*4=25=5^2
x=(7+5)/2=6
x=(7-5)/2=1
Проверка: подставляем в исходное уравнение
х=6
 +6+3=6
+6+3=6
3+6+3=6
корень не подходит
х=1
 +1+3=6
+1+3=6
2+1+3=6
Ответ х=1
3 +
+ =0
=0
сумма положительных чисел будет равна 0 если каждое слогаемое равно 0, х2=0, х=0. но тогда =
=
решений нет.
можно еще по другому, возвести в квадрат обе части и прийти к отрицательному дискриминанту
возводим в квадрат обе части уравнени
х+3=(3-х)^2
x+3=9-6x+
D-49-6*4=25=5^2
x=(7+5)/2=6
x=(7-5)/2=1
Проверка: подставляем в исходное уравнение
х=6
3+6+3=6
корень не подходит
х=1
2+1+3=6
Ответ х=1
3
сумма положительных чисел будет равна 0 если каждое слогаемое равно 0, х2=0, х=0. но тогда
решений нет.
можно еще по другому, возвести в квадрат обе части и прийти к отрицательному дискриминанту
oganesbagoyan:
3 - х ≥ 0
Автор ответа:
0
task/28159560
-------------------
2.
√ (x+3) + (x+3) =6 ;
ОДЗ : x+3 ≥ 0 ⇒ x ∈ [ -3 ; ∞)
* * * (√(x+3) )² + √ (x+3) - 6 =0 квадратное уравнение отн. √ (x+3) * * *
замена: t = √(x+3) ≥ 0 .
t² +t - 6 =0 ⇔ t² -(-3+2)t +(-3)*2 =0 * * * Виет * * *
* * * или D = 1² -4*1(-6) = 25 =5² ; t₁ = (-1-5)/2= -3 ; t₂ = (-1+5)/2=2 * * *
t₁ = -3 < 0 _посторонный корень
t₂ = 2 ⇒ √(x+3) =2 ⇔ x+3 =2² ⇔ x=1.
ответ: x=1.
------------------------
3.
√ (x²+2) + x² =0 ;
√ (x²+2) ≥ √2 и x² ≥ 0 , следовательно √ (x²+2) +x² ≥ √2
Уравнение не имеет решения.
ответ : x ∈ ∅ .
-------------------
2.
√ (x+3) + (x+3) =6 ;
ОДЗ : x+3 ≥ 0 ⇒ x ∈ [ -3 ; ∞)
* * * (√(x+3) )² + √ (x+3) - 6 =0 квадратное уравнение отн. √ (x+3) * * *
замена: t = √(x+3) ≥ 0 .
t² +t - 6 =0 ⇔ t² -(-3+2)t +(-3)*2 =0 * * * Виет * * *
* * * или D = 1² -4*1(-6) = 25 =5² ; t₁ = (-1-5)/2= -3 ; t₂ = (-1+5)/2=2 * * *
t₁ = -3 < 0 _посторонный корень
t₂ = 2 ⇒ √(x+3) =2 ⇔ x+3 =2² ⇔ x=1.
ответ: x=1.
------------------------
3.
√ (x²+2) + x² =0 ;
√ (x²+2) ≥ √2 и x² ≥ 0 , следовательно √ (x²+2) +x² ≥ √2
Уравнение не имеет решения.
ответ : x ∈ ∅ .
Похожие вопросы
Предмет: Биология,
автор: Layladragoshani
Предмет: Окружающий мир,
автор: irinastepanova6066
Предмет: Математика,
автор: regina22opimah
Предмет: Алгебра,
автор: doloreshaze
Предмет: История,
автор: zinovksu