Предмет: Геометрия, автор: Аноним

Богом прошу, помогите с геометрией?
Прямоугольный треугольник АВС (∠В = 90°) перегнули по его медиане ВМ так, что плоскости ВАМ и ВМС оказались перпендикулярными. Найдите расстояние между точками А и С, если АВ = 12 см, сos∠BAM = 3/5.

Аноним: NikitatheBest313, ты в адеквате?

Аноним: Я так понимаю, мне никто ничего не объяснит...

Аноним: и где?

Аноним: я решу, не переживай

AnonimusPro: Я отвечаю на вопрос, если уверен в своем ответе на 100%.Здесь я сомневаюсь в своем ответе. Лучше пусть кто-нибудь другой ответит.

Аноним: В Г Д З такой же ответ (10√2), я думаю это правильно

AnonimusPro: И в Г Д З ошибаются. Причем очень часто.

Аноним: Кстати, у меня есть 2 Г Д З и в этом задании у них разные ответы...

Аноним: я пока решаю еще, не отмечайте нарушение-а то заблокируется ответ

Ответы

Автор ответа: Аноним

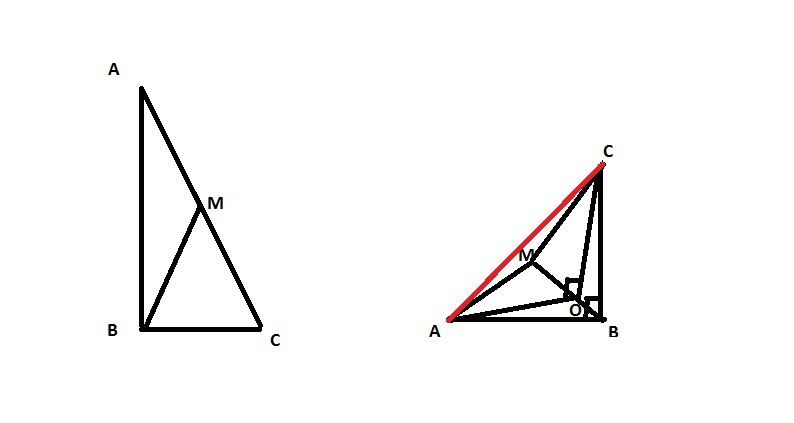
На представленном рисунке дан ΔАВС до сгиба и после
До сгиба нужно определить гипотенузу АС и катет ВС
AC=AB/cos BAC=12/0.6=20
BC^2=AC^2-AB^2=20^2-12^2=400-144=256
BC=16
Теперь о перегибе: необходимо найти проекцию вершины А при cгибе по медиане ВМ на плоскость АВМ, это точка О на втором рисунке
ΔАОС -будет прямоугольный и тогда по т. Пифагора я найду АС
Чтобы определить тоску О, я из вершины А опускаю перпендикуляр на ВМ и нахожу СО
CO-высота в BMC, CO=BC*sinMBC
SinMBC=0.6(ΔBMC-равнобедренный h=√(10^2-8^2)=6; sinMBC=h/BM=6/10=0/6)
CO=16*0,6=9.6
BO^2=BCBC^2-CO^2=256-92.16=163.84
BO=12.8
OA^2=BO^2+AB^2-2*AB*BO*Cos(90-<MBC)=163.84+144-2*12*12.8*0.6=123.52
AC^2=OA^2+OB^2=123.52+162.84=286.36
AC≈16.92

Приложения: