Предмет: Алгебра,
автор: Целый
Найти производную сложной функции (с решением, а не просто ответ)
Спасибо!
Приложения:
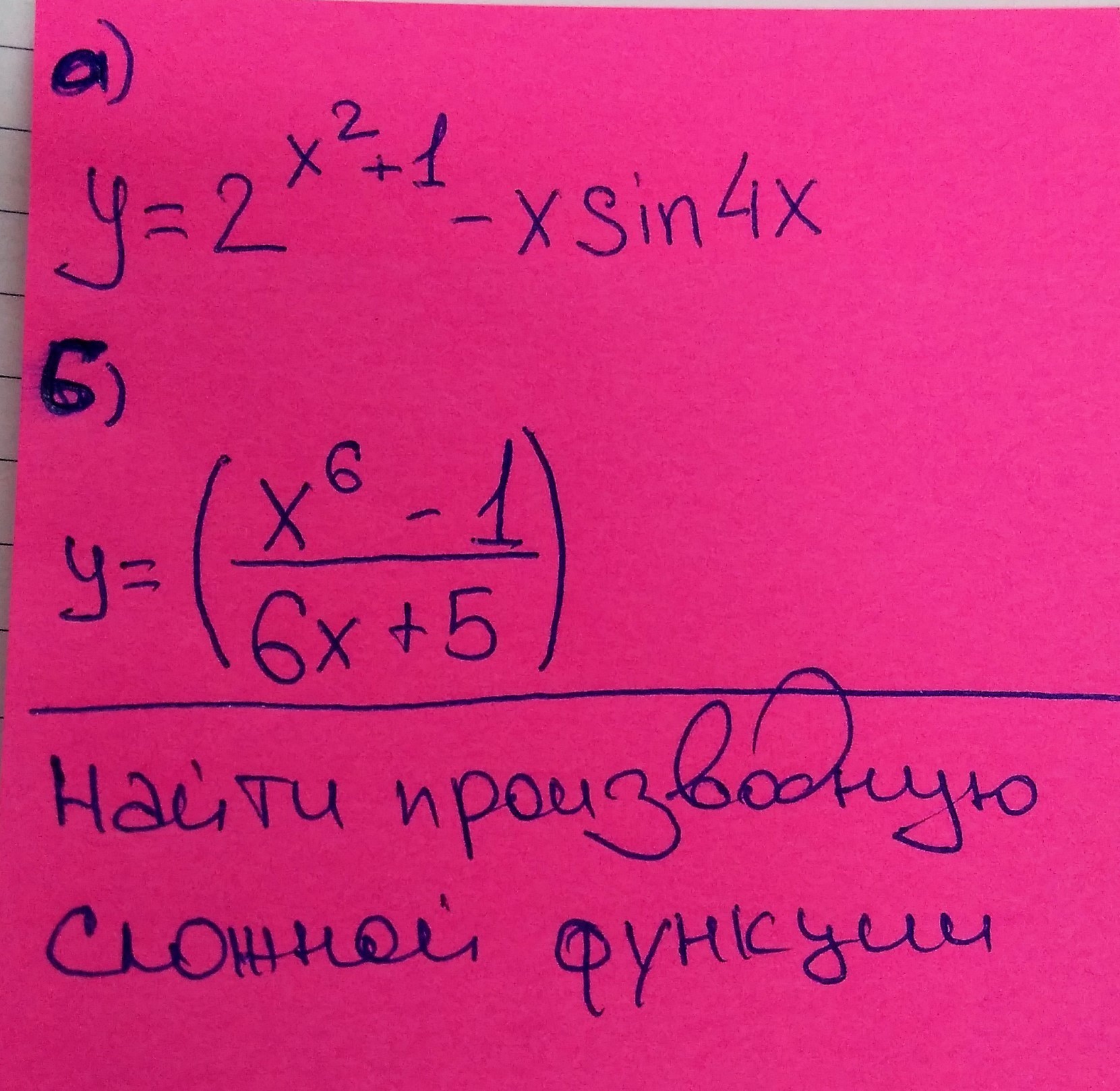
Ответы
Автор ответа:
0
какой класс?))))))))
Целый:
техникум
Автор ответа:
0
))y=2^(x²+1)-xsin4x
2^(x²+1)'=2^(x²+1)*2x*ln2
xsin4x'=u'v+v'u u=x u'=1 v=sin4x v'=4cos4x
xsin4x'=1*sin4x+4xcos4x
y'=2^(x²+1)*2x*ln2+sin4x+4xcos4x
y'=1/v²[u'v-v'u] u=(x⁶-1) u'=6x⁵ v=6x+5 v'=6
y'=1/(6x+5)²[6x⁵(6x+5)-6(x⁶-1)]
2^(x²+1)'=2^(x²+1)*2x*ln2
xsin4x'=u'v+v'u u=x u'=1 v=sin4x v'=4cos4x
xsin4x'=1*sin4x+4xcos4x
y'=2^(x²+1)*2x*ln2+sin4x+4xcos4x
y'=1/v²[u'v-v'u] u=(x⁶-1) u'=6x⁵ v=6x+5 v'=6
y'=1/(6x+5)²[6x⁵(6x+5)-6(x⁶-1)]
Похожие вопросы
Предмет: Математика,
автор: polakovavaleroa54
Предмет: Қазақ тiлi,
автор: kolezadi19
Предмет: Українська література,
автор: yasichka45
Предмет: Математика,
автор: vladkharitonov2