Предмет: Алгебра,
автор: Anastasiya201295
помогите решить пожалуйста подробно
Приложения:
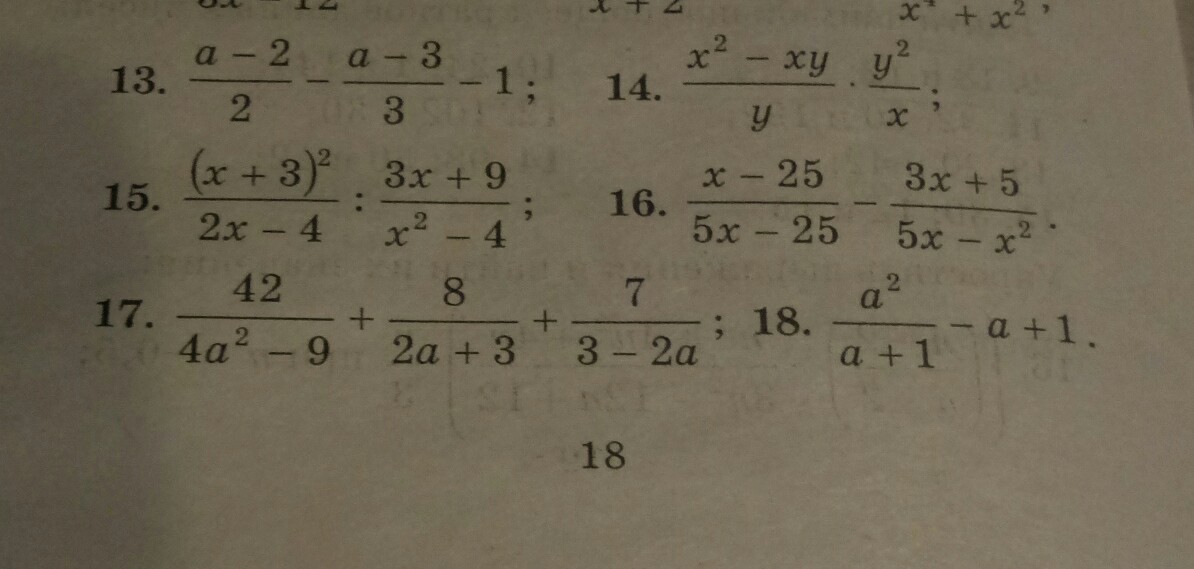
Ответы
Автор ответа:
0
Вот и всё решение........
Приложения:

Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: dayana3112
Предмет: Химия,
автор: HxTTwaY
Предмет: Алгебра,
автор: dzurykveronika2605
Предмет: Алгебра,
автор: 10224
Предмет: Обществознание,
автор: лоллл2