Question

f(x)= x^2 + bx (b больше нуля)
начертите фигуру, ограниченную осью х и линией f(x). В фигуру вписан прямоугольный треугольник, у которого одна вершина лежит в начале координат, один из катетов на оси х, а противоположная ему вершина - на линии f(x). найдите максимальную площадь этого треугольника.

Задача вроде решается, а только х в итоге может расти бесконечно( то есть максимальная площадь не имеет конца). Предложите, пожалуйста, ваш вариант решения.
p.s. желательно без использования второй производной, а через луч. Так нагляднее.
Заранее спасибо!

Answer 1

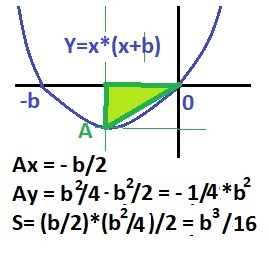
РЕШЕНИЕ на рисунке в приложении.
Разложили функцию на множители
Y = x*(x+b)
Корни функции - точки пересечения с осью Х
х = 0, х = - b
Вершина параболы по середине между корнями.
Строим прямоугольный треугольник к вершине параболы и именно он будет иметь максимальную площадь.
ОТВЕТ Smax = b³/16