Question

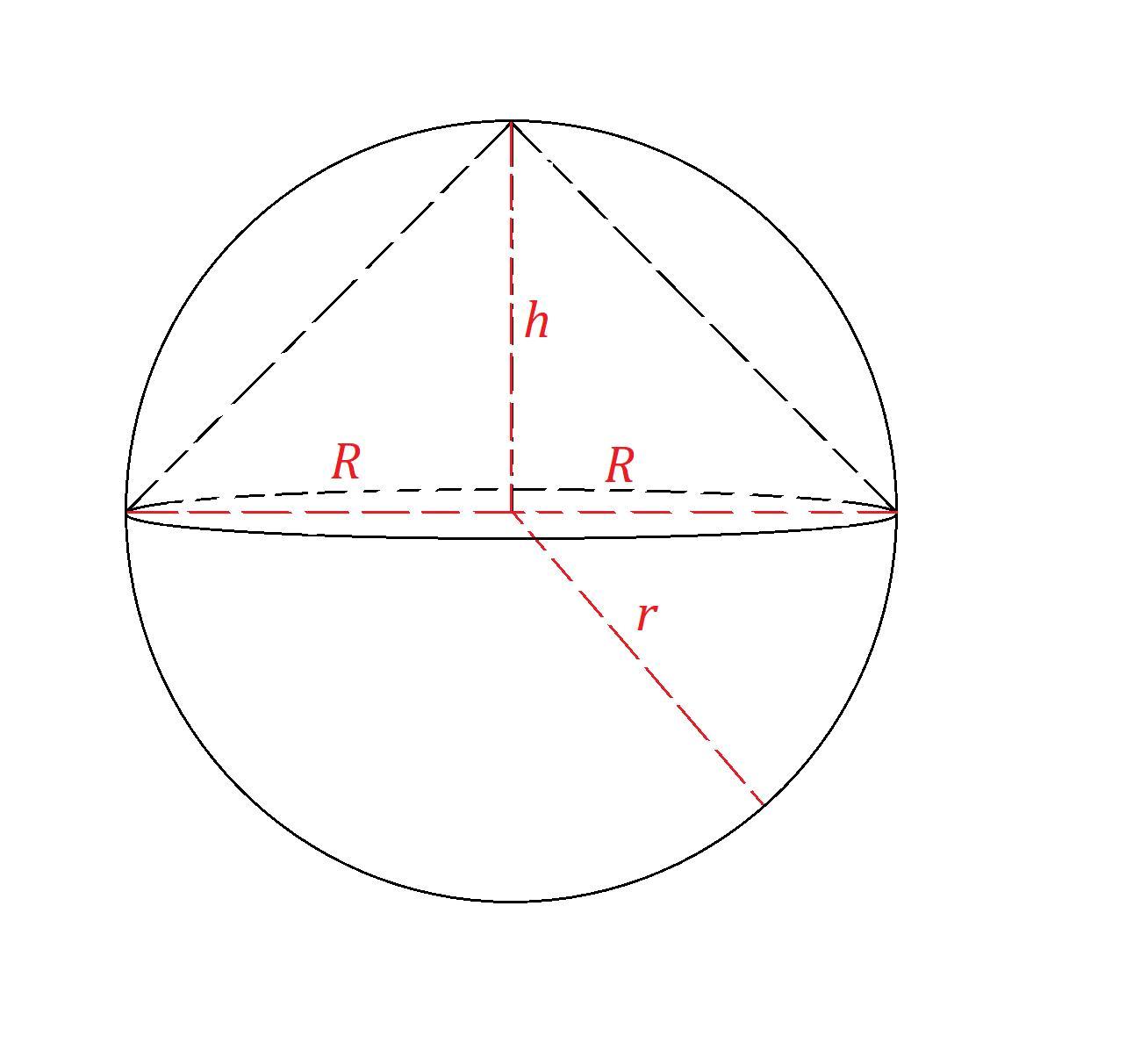
Конус вписан в шар. Высота конуса равна радиусу шара. Объем конуса равен 8. Найдите объем шара.

Answer 1

Ответ:

$V_2 = 32$.

Объяснение:

Пусть $R$ - радиус основания конуса, $h$ - высота конуса, $r$ - радиус шара,  $V_1$ - объём конуса, $V_2$ - объём шара.

По условию, $h = r \Rightarrow R = r = h$.

$V_1 = \dfrac{1}{3} * \pi * R^{2}* h = \dfrac{1}{3} * \pi * R^{3}$, так как $R = h$.

$V_2 = \dfrac{4}{3} * \pi * r^{3}$

Исходя из обеих формул заметим, что нам достаточно узнать чему равно $R^{3}$ или $r^{3}$, чтобы найти объём шара.

$\Rightarrow R^{3} = \dfrac{V_1 * 3}{\pi} = \dfrac{8 * 3}{\pi} = \dfrac{24}{\pi}$

$R^{3} = r^{3} = \dfrac{24}{\pi}$

$\Rightarrow V_2 = \dfrac{4}{3} *\pi *\dfrac{24}{\pi} = \dfrac{4}{3} * 24= 4 * 8 = 32$