Question

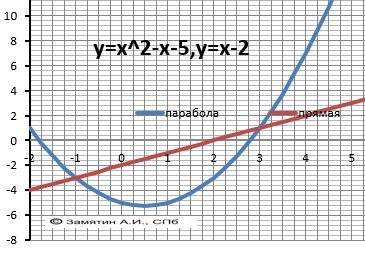
Вычислите площадь фигуры, ограниченной линиями a)y=x^2-x-5, y=x-2
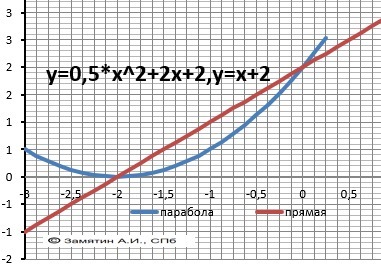
б)y=0.5x^2+2x+2, y=x+2

Answer 1

ДУМАЕМ
1. Площадь - интеграл разности функций. 
2. Парабола положительная - ветви вверх - значит прямая выше - от уравнения прямой вычитаем уравнение параболы.
РЕШЕНИЕ
1)
Находим пределы интегрирования решая уравнение.
(x-2) - (x²-x - 5) = 0
a = 3, b = - 1
Уравнение площади - интеграл разности функций.
$S= \int\limits^a_b {(3+2x-x^2)} \, dx=\frac{3x}{1}+ \frac{2x^2}{2}- \frac{x^3}{3}$
Вычисляем на границах интегрирования.
S(3) = 9 + 9 - 9 = 9
S(-1) = -3+1 + 1/3 = -1 2/3
S=S(3)-S(-1) = 9 - (-1 2/3) = 10 2/3 - площадь - ОТВЕТ
Рисунок к задаче в приложении.
2) Пределы интегрирования
0,5*x² + x = 0
a = 0, b = -2
Интеграл разности функций.
$S= \int\limits^a_b {(-x-x^2)} \, dx=- \frac{x^2}{2}- \frac{x^3}{3}$
S(0) = 0, S(-2) = -2/3
S = 2/3 - площадь - ОТВЕТ