Предмет: Математика,
автор: dashadomrachev
Решить неравенство . ХЕЛП ПЛИИЗ
Приложения:
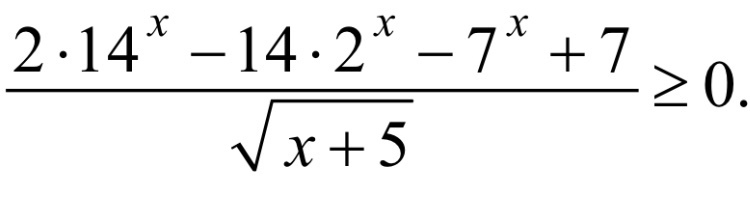
Ответы
Автор ответа:
0
Область определения квадратного корня в знаменателе: x > -5.
Сам корень арифметический, то есть неотрицательный, поэтому
2*14^x - 14*2^x - 7^x + 7 >= 0
2*2^x*7^x - 2*7*2^x - 7^x + 7 >= 0
2*2^x*(7^x - 7) - (7^x - 7) >= 0
(7^x - 7)(2*2^x - 1) >= 0
Возможны 2 случая:
1) Обе скобки отрицательны
{ 7^x - 7 <= 0
{ 2*2^x - 1 <= 0
Переносим числа направо. Второе уравнение делим на 2
{ 7^x <= 7; x <= 1
{ 2^x <= 1/2; x<= -1
Получаем: x ∈ (-5; -1]
2) Обе скобки положительны
{ 7^x - 7 >= 0
{ 2*2^x - 1 >= 0
Решаем точно также.
{ x >= 1
{ x >= -1
Получаем x ∈ [1; +oo)
Ответ: (-5; -1] U [1; +oo)
Сам корень арифметический, то есть неотрицательный, поэтому
2*14^x - 14*2^x - 7^x + 7 >= 0
2*2^x*7^x - 2*7*2^x - 7^x + 7 >= 0
2*2^x*(7^x - 7) - (7^x - 7) >= 0
(7^x - 7)(2*2^x - 1) >= 0
Возможны 2 случая:
1) Обе скобки отрицательны
{ 7^x - 7 <= 0
{ 2*2^x - 1 <= 0
Переносим числа направо. Второе уравнение делим на 2
{ 7^x <= 7; x <= 1
{ 2^x <= 1/2; x<= -1
Получаем: x ∈ (-5; -1]
2) Обе скобки положительны
{ 7^x - 7 >= 0
{ 2*2^x - 1 >= 0
Решаем точно также.
{ x >= 1
{ x >= -1
Получаем x ∈ [1; +oo)
Ответ: (-5; -1] U [1; +oo)
Похожие вопросы
Предмет: Английский язык,
автор: timurnadezdi
Предмет: Литература,
автор: vitalinakostiukevych
Предмет: Химия,
автор: Аноним
Предмет: Обществознание,
автор: крутой127