Предмет: Алгебра,
автор: Voleal
Найти самое большое значение n, при котором следующее выражение имеет натуральное значение:
![\sqrt[n]{ {81}^{2} + {9}^{4} + {3}^{8} } \sqrt[n]{ {81}^{2} + {9}^{4} + {3}^{8} }](https://tex.z-dn.net/?f=+%5Csqrt%5Bn%5D%7B+%7B81%7D%5E%7B2%7D++%2B++%7B9%7D%5E%7B4%7D+%2B++%7B3%7D%5E%7B8%7D++%7D+)
Ответ 3, я просто не знаю как он получился. Вот решение. Последний шаг я не могу понять. Объясните пожалуйста
Приложения:
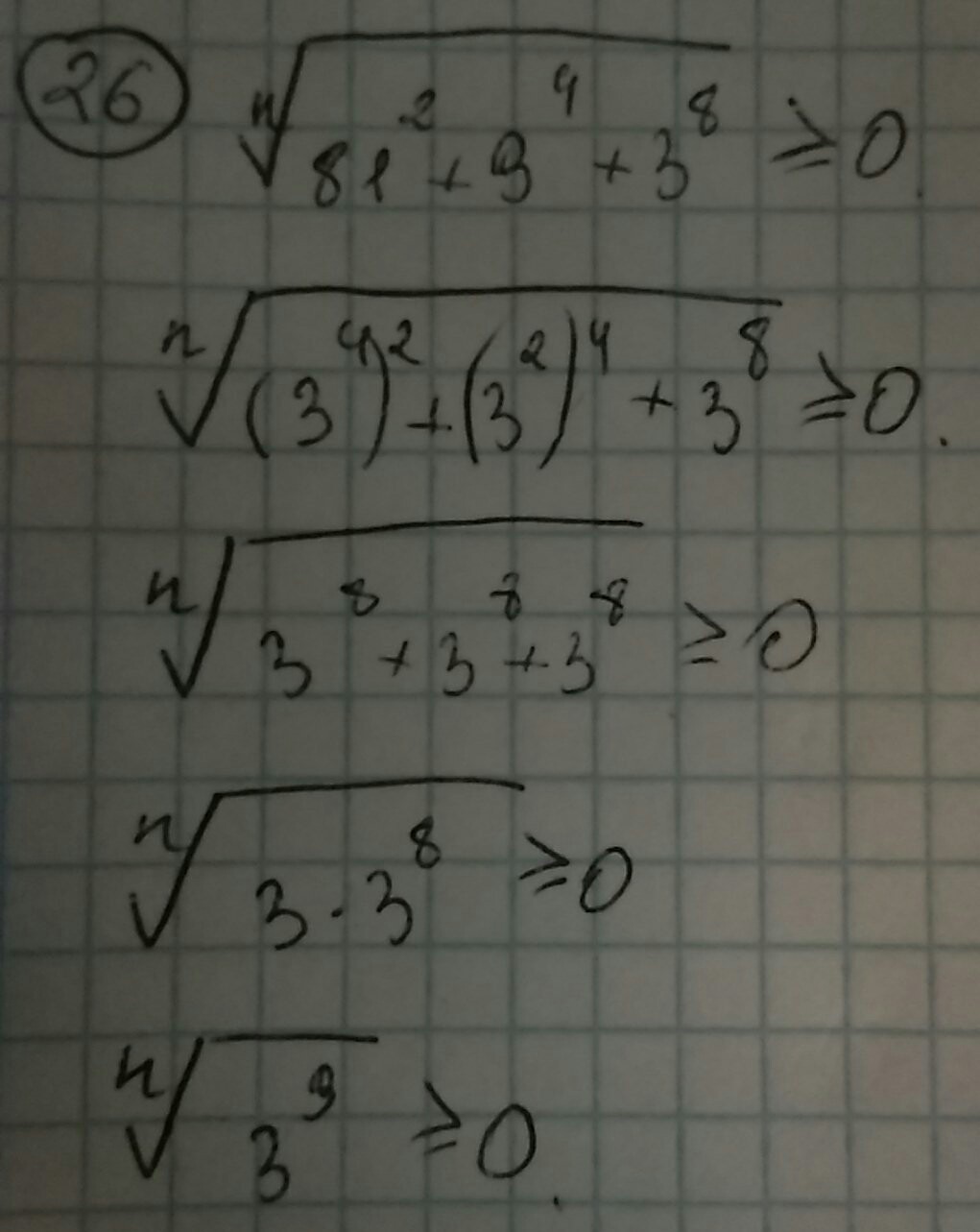
Voleal:
извеняюсь, знак "нестрого больше нуля" не нужен. это не неравенство
Ответы
Автор ответа:
2
9 должно быть кратно n, чтобы получить натуральное значение, значит, n=3 или 9. При n=3 выражение будет равно 3^(9/3)=3³=27, при n=9 выражение будет равно 3^(9/9)=3¹=3
3<9
Ответ: n=9
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Литература,
автор: nurzhan20070607
Предмет: Литература,
автор: kadyrbaimadina10
Предмет: Математика,
автор: Абурбубяка
Предмет: Геометрия,
автор: svetic1980