Question

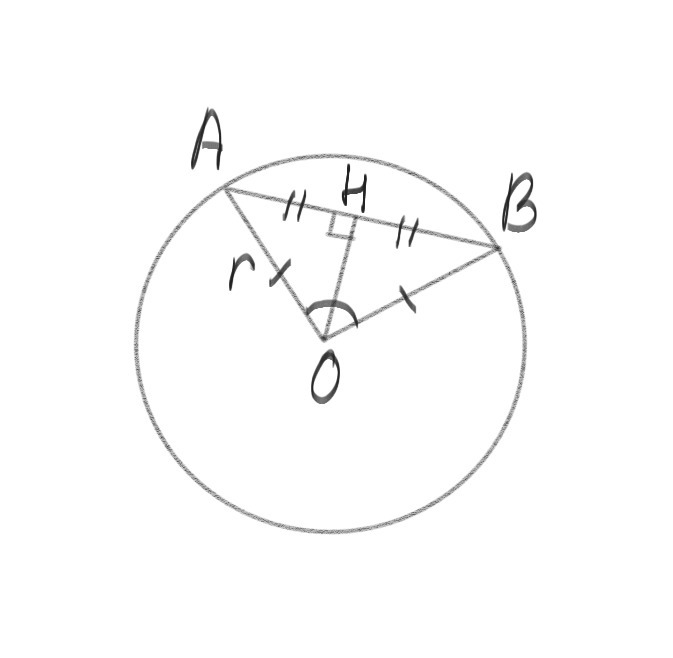
Расстояние от центра окружности О до хорды АВ вдвое меньше радиуса окружности. Найти угол АОВ.
(7 класс)

Answer 1

ОН⊥АВ
Пусть ОН=х, тогда АО=2х
ΔАОН - прямоуг. (∠АНО=90°)
ОН=1/2 АО => ∠ОАН=30°
∠АОН=90°-∠ОАН=90°-30°=60°

ΔАВО - р/б (ОА=ОВ=r)
ОН⊥АВ => ОН - биссектриса ΔАВО
∠АОН=∠НОВ=60°
∠АОВ=∠АОН+∠НОВ=60°+60°=120°