Предмет: Геометрия,
автор: DOGY228
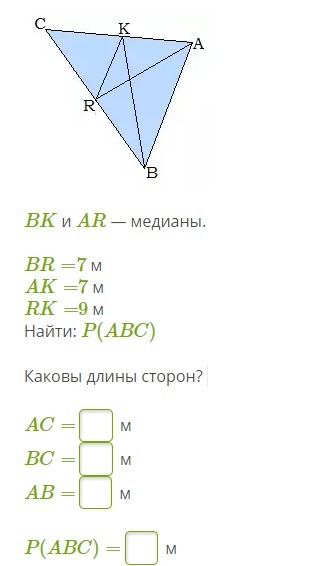
BK и AR — медианы.
BR=7 м
AK=7 м
RK=9 м
Найти: P(ABC)
Каковы длины сторон?
AC=?м
BC=?м
AB=?м
P(ABC)=?м
Приложения:
DOGY228:
Помогите с вопросом task/28149699
Ответы
Автор ответа:
15
Решение смотри на фото:
Приложения:
помоги с вопросом task/28149699
Автор ответа:
8
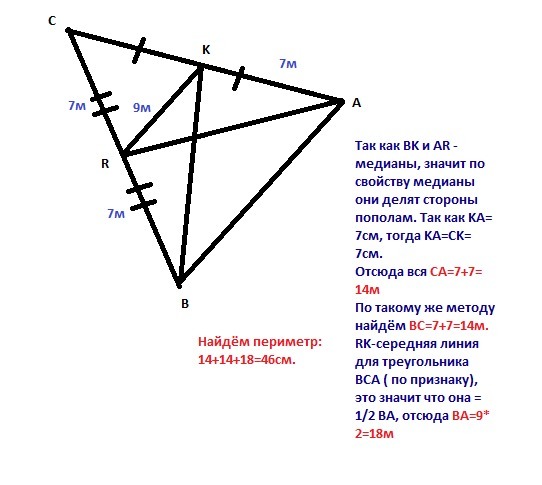
Так как BK и AR — медианы, значит, что СК = КА и СR = RB.
Значит, что СА = 7 + 7 = 14; а СВ = 7 + 7 = 14;
У нас есть 2 треугольника АВС и СRК с однаково пропорциональными сторонами
АС : СК = 14 : 7 и СВ : СR = 14 : 7. Так как угол между сторонами (СR СК) и (СВ СА) одинаковый значит треугольники подобные, а их соответствующие стороны пропорциональные на k = 14 : 7 = 2;
Значит АВ = RК * 2 = 18
Р(АВС) = 18 + 14 + 14 = 46 м
Значит, что СА = 7 + 7 = 14; а СВ = 7 + 7 = 14;
У нас есть 2 треугольника АВС и СRК с однаково пропорциональными сторонами
АС : СК = 14 : 7 и СВ : СR = 14 : 7. Так как угол между сторонами (СR СК) и (СВ СА) одинаковый значит треугольники подобные, а их соответствующие стороны пропорциональные на k = 14 : 7 = 2;
Значит АВ = RК * 2 = 18
Р(АВС) = 18 + 14 + 14 = 46 м
Помоги с вопросом task/28149699
Похожие вопросы
Предмет: Информатика,
автор: artemkaplau
Предмет: Математика,
автор: butuzovgrisha
Предмет: Химия,
автор: madi6677
Предмет: Литература,
автор: kolya555kolya
Предмет: Информатика,
автор: anko304