Предмет: Информатика,
автор: zhivotov1960
Даны 4 целых числа, записанные в двоичной системе:
10001011, 10111000, 10011011, 10110100.
Сколько среди них чисел, больших, чем A4(16)+20(8)?
в скобках даны системы счисления.
Ответы
Автор ответа:
2
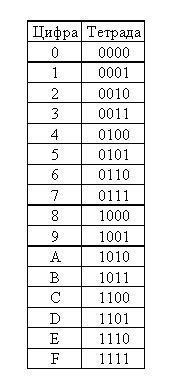
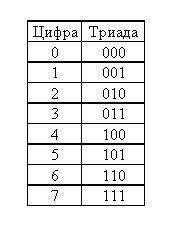
Пользуясь таблицами триад и тетрад, переведем числа в двоичную систему счисления, посчитаем сумму A4(16) и 20(8). Получаем число 10110100(2).
Далее числа можно сравнить по первым четырем цифрам. У полученной суммы это "1011".
Для удобства разделим числа на разряды по четыре цифры.
1) 1000 1011.
2) 1011 1000.
3) 1001 1011.
4) 1011 0100.
Из данных чисел видим, что варианты под 1 и 3 номерами не подходят (т.к. 1000 < 1011 и 1001 < 1011, смотри таблицу тетрад).
Остаются два варианта:
2) 1011 1000.
4) 1011 0100.
Видя, что четвертый вариант ответа совпадает с нашей суммой, можем сделать вывод, что нам подходит только число 1011 1000.
Ответ: одно число.
Далее числа можно сравнить по первым четырем цифрам. У полученной суммы это "1011".
Для удобства разделим числа на разряды по четыре цифры.
1) 1000 1011.
2) 1011 1000.
3) 1001 1011.
4) 1011 0100.
Из данных чисел видим, что варианты под 1 и 3 номерами не подходят (т.к. 1000 < 1011 и 1001 < 1011, смотри таблицу тетрад).
Остаются два варианта:
2) 1011 1000.
4) 1011 0100.
Видя, что четвертый вариант ответа совпадает с нашей суммой, можем сделать вывод, что нам подходит только число 1011 1000.
Ответ: одно число.
Приложения:
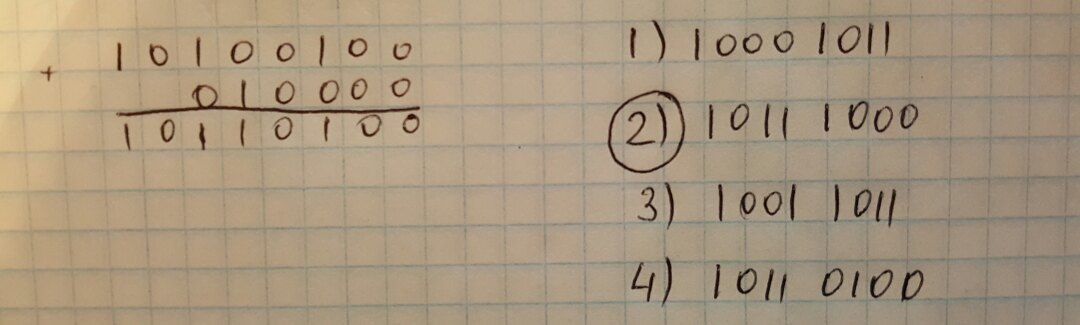
Похожие вопросы
Предмет: Алгебра,
автор: a9269618367
Предмет: Физика,
автор: cubecat14081408
Предмет: Английский язык,
автор: sanea20052
Предмет: Математика,
автор: Мирвари1