Предмет: Математика,
автор: topgamerinthewo1Xi
Формула Ньютона-Лейбинца
Приложения:
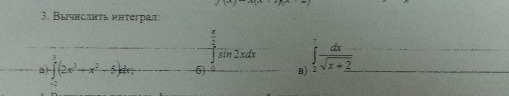
Ответы
Автор ответа:
0
Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием интеграла Римана и вычислением первообразной.
Если {\displaystyle \textstyle f(x)} непрерывна на отрезке {\displaystyle \left[a,b\right]} и {\displaystyle \textstyle \Phi (x)} — её любая первообразная на этом отрезке, то имеет место равенство
{\displaystyle \int \limits _{a}^{b}f(x)dx=\Phi (b)-\Phi (a)={\Bigl .}\Phi (x){\Bigl |}_{a}^{b}}
Если {\displaystyle \textstyle f(x)} непрерывна на отрезке {\displaystyle \left[a,b\right]} и {\displaystyle \textstyle \Phi (x)} — её любая первообразная на этом отрезке, то имеет место равенство
{\displaystyle \int \limits _{a}^{b}f(x)dx=\Phi (b)-\Phi (a)={\Bigl .}\Phi (x){\Bigl |}_{a}^{b}}
yugolovin:
От Вас требовалось найти интегралы с помощью формулы Ньютона-Лейбница
Похожие вопросы
Предмет: Английский язык,
автор: lesyabazyuk
Предмет: Английский язык,
автор: romazudin37
Предмет: Английский язык,
автор: alihanadil00
Предмет: Математика,
автор: evkme
Предмет: Алгебра,
автор: vays78