Question

Шар вписан в цилиндр . Площадь поверхности шара равна 32 . Найдите площадь полной поверхности цилиндра

Answer 1

Площадь поверхности шара равна 32:    S шара = 4πR²   ⇒
4πR² = 32;   πR² = 32/4 = 8
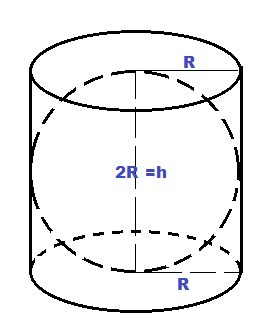
Шар вписан в цилиндр, значит, радиус основания цилиндра равен радиусу шара, а высота равна диаметру шара   h = 2R
Площадь основания цилиндра  S₀=πR² = 8
Площадь боковой поверхности цилиндра
Sбок = 2π R h = 2π R*2R = 4πR² = 32

Площадь полной поверхности цилиндра
S = Sбок + 2S₀ = 32 + 2*8 = 48

Ответ: S = 48 кв.ед.