Question

Пирамида пересечена плоскостью, параллельной основанию, которая делит высоту пирамиды в отношении 3:8, считая от вершины.
Вычисли площадь основания, если площадь сечения равна 27дм2.

Answer 1

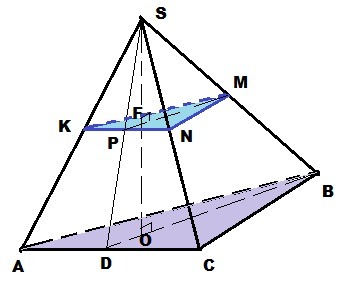
Для наглядности привожу рисунок треугольной пирамиды, хотя она может быть какой угодно.

Пирамида SABC;  высота  SO⊥(ABC);  (KMN)║(ABC);  SF:FO = 3:8
$S_{KMN}=27$  дм²
$\frac{SF}{FO} = \frac{3}{8}$      $FO= \frac{8}{3} SF$     
SO = SF + FO = SF +  $\frac{8}{3} SF = \frac{11}{3} SF$

ΔSFM  прямоугольный  ∠SFM = 90°
ΔSOB  прямоугольный  ∠SOB = 90°
ΔSFM ~ ΔSOB  по общему острому ∠FSM  ⇒
$\frac{SB}{SM} = \frac{SO}{SF} = \frac{ \frac{11}{3} SF}{SF} = \frac{11}{3}$

NM║CB  ⇒ ∠SNM = ∠SCB; ∠SMN = ∠SBC как соответственные углы  ⇒
ΔSCB ~ ΔSNM  по двум равным углам   ⇒
$\frac{CB}{NM} = \frac{SB}{SM} = \frac{11}{3}$   ⇒
Т.к. фигура в сечении пирамиды плоскостью, параллельной основанию, подобна основанию, то ΔABC ~ ΔKMN с коэффициентом подобия
k = $\frac{11}{3}$
Площади подобных фигур относятся как коэффициент подобия в квадрате
$\frac{S_{ABC}}{S_{KMN}} =k^2=( \frac{11}{3} )^2= \frac{121}{9} \\ \\ S_{ABC}= \frac{121}{9} S_{KMN}= \frac{121}{9} *27=363$

Ответ: площадь основания 363 дм³