Предмет: Алгебра,
автор: Emily0118
Объясните пожалуйста принцип решения номера на одном из 4 примеров, желательно расписав решение на бумаге) (тема "Свойства логарифмов")
Приложения:
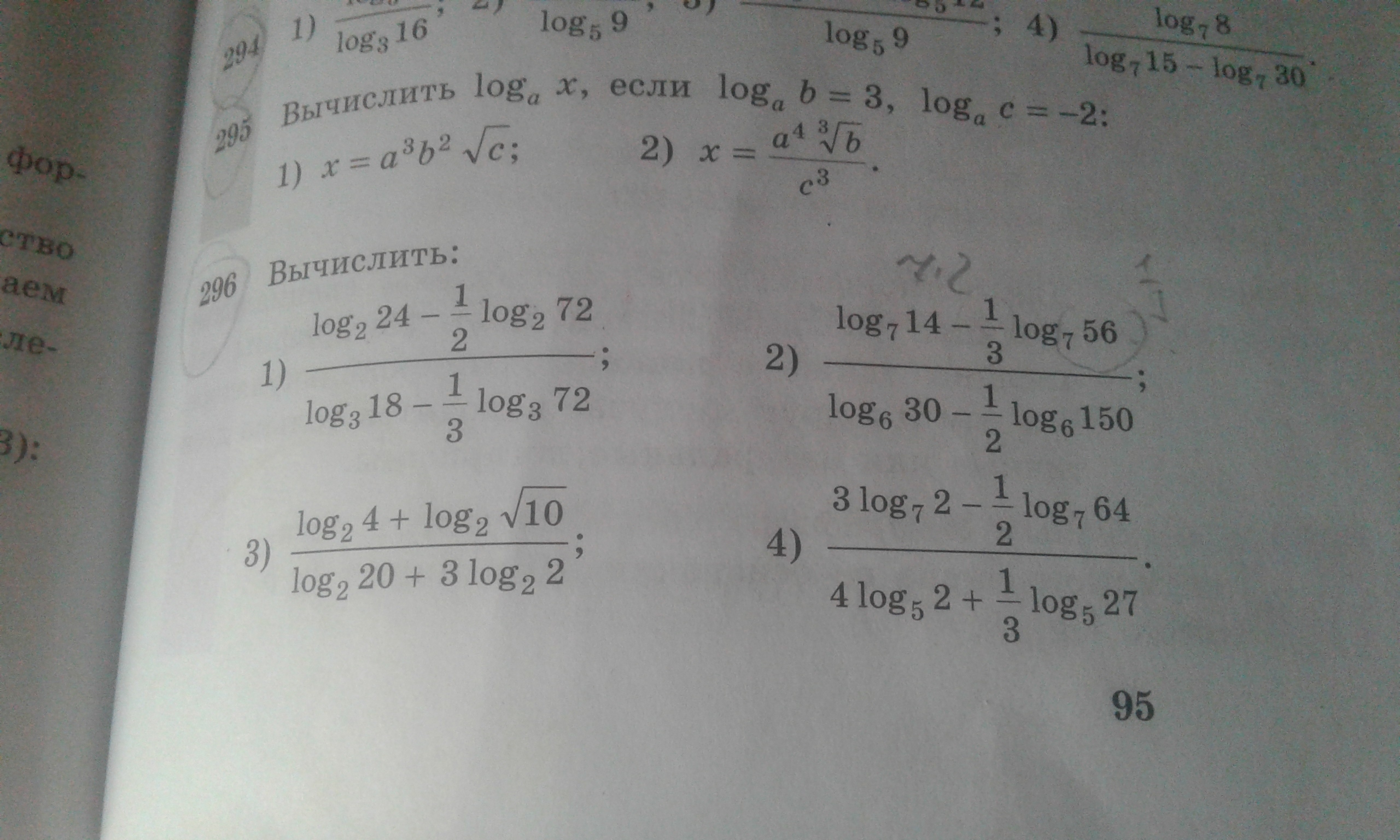
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Алгебра,
автор: kazumuhankilibaev
Предмет: Математика,
автор: oleinikova198317
Предмет: Английский язык,
автор: arynovab76
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: ENZHE62