Предмет: Алгебра,
автор: nikataaa
ПОМОГИТЕ ПОЖАЛУЙСТА, ОЧЕНЬ СРОЧНО
Приложения:
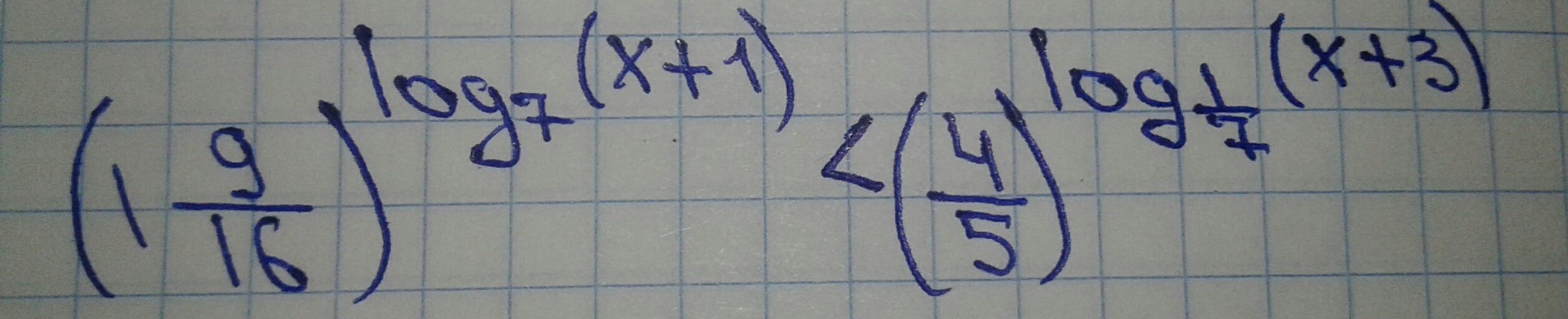
Ответы
Автор ответа:
0
Основание больше 1
__+___ - 2 __-___ 1 ____+____ (-2;1)
и ОДЗ
__________-1 ___+___________ x>-1
ОТВЕТ (-1;1)
Похожие вопросы
Предмет: Математика,
автор: nesibelikotova
Предмет: Литература,
автор: anosovvova7
Предмет: Английский язык,
автор: stiharnynikita
Предмет: Химия,
автор: sabanaev234
Предмет: География,
автор: abu7071