Предмет: Алгебра,
автор: Нникто
Докажите, что при любых значениях переменных справедливо неравенство на фото.
Умоляю, очень сложно.
ДАЮ 80 БАЛЛОВ.
Заранее благодарю.
Приложения:
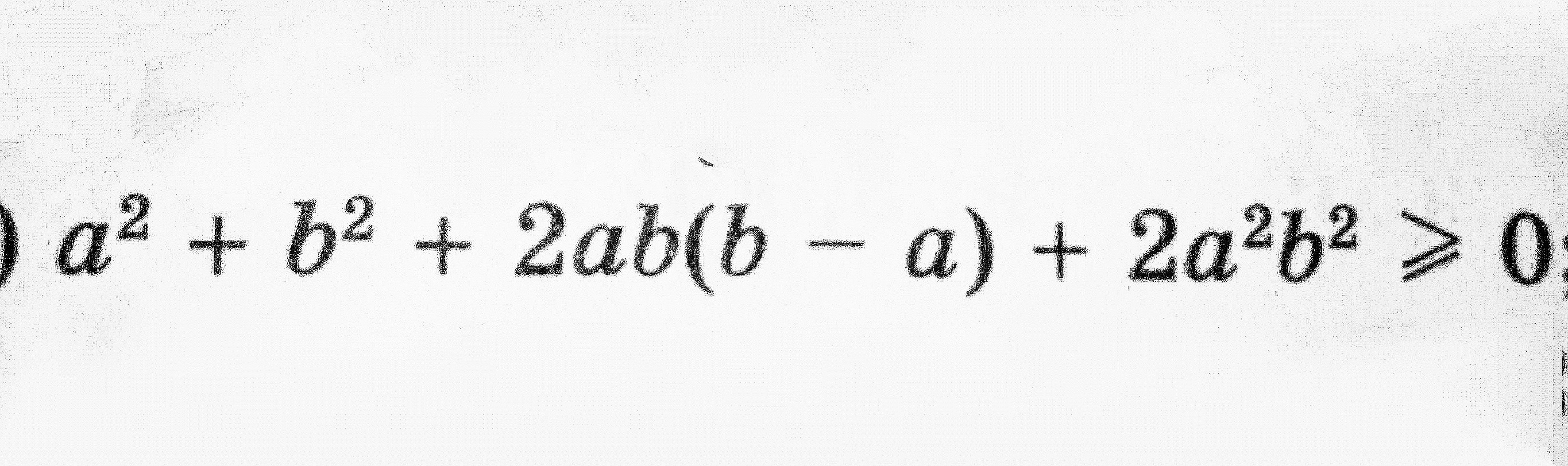
???
Ответы
Автор ответа:
0
У нас есть член 2ab(b - a). Можно предположить, что это член квадрата
(b - a + ab)^2 = (b - a)^2 + 2ab(b - a) + a^2*b^2
Теперь раскрываем скобки и получаем:
a^2 + b^2 - 2ab + 2ab(b - a) + a^2*b^2
Подставляем это в наше выражение, которое мы обозначим N:
N = a^2 + b^2 + 2ab(b - a) + 2a^2*b^2 =
= a^2 + b^2 + 2ab(b - a) + a^2*b^2 - 2ab + 2ab + a^2*b^2 =
= (b - a + ab)^2 + 2ab + a^2*b^2 = (b - a + ab)^2 + ab*(ab + 2)
Первая скобка - квадрат, он неотрицателен при любых a и b.
Второе произведение - результат умножения числа ab на ab + 2.
1) Если ab >= 0, то ab + 2 > 0, и произведение ab*(ab + 2) >= 0.
2) Если ab <= -2 < 0, то ab + 2 <= 0, и произведение ab*(ab + 2) тоже >= 0.
3) Если ab < 0, и ab + 2 > 0, то, например, ab = -1, ab + 2 = 1, тогда
а) a = -1; b = 1; N = (b-a+ab)^2 + ab*(ab+2) = (1+1-1)^2 + (-1)*1 = (-1)^2 - 1 = 0
б) a = 1; b = -1; N = (-1-1-1)^2 + (-1)*1 = (-3)^2 - 1 = 8
в) Или, например, ab = -1,5; ab + 2 = 0,5, тогда
a = 3; b = -0,5; N = (-0,5-3-1,5)^2 + (-1,5)*(0,5) = (-5)^2 - 0,75 = 24,25
г) Если, например, ab = -0,5; ab + 2 = 1,5, тогда
a = 0,5; b = -1; N = (-1-0,5-0,5)^2 + (-0,5)*(1,5) = (-2)^2 - 0,75 = 3,25
В любом случае, если произведение ab < 0 и ab + 2 > 0, то указанное выражение неотрицательно.
В пунктах 1) и 2) вычислили, что при ab >= 0 и при ab <= -2 выражение тоже неотрицательно.
Таким образом, мы доказали, что оно неотрицательно в любом случае.
(b - a + ab)^2 = (b - a)^2 + 2ab(b - a) + a^2*b^2
Теперь раскрываем скобки и получаем:
a^2 + b^2 - 2ab + 2ab(b - a) + a^2*b^2
Подставляем это в наше выражение, которое мы обозначим N:
N = a^2 + b^2 + 2ab(b - a) + 2a^2*b^2 =
= a^2 + b^2 + 2ab(b - a) + a^2*b^2 - 2ab + 2ab + a^2*b^2 =
= (b - a + ab)^2 + 2ab + a^2*b^2 = (b - a + ab)^2 + ab*(ab + 2)
Первая скобка - квадрат, он неотрицателен при любых a и b.
Второе произведение - результат умножения числа ab на ab + 2.
1) Если ab >= 0, то ab + 2 > 0, и произведение ab*(ab + 2) >= 0.
2) Если ab <= -2 < 0, то ab + 2 <= 0, и произведение ab*(ab + 2) тоже >= 0.
3) Если ab < 0, и ab + 2 > 0, то, например, ab = -1, ab + 2 = 1, тогда
а) a = -1; b = 1; N = (b-a+ab)^2 + ab*(ab+2) = (1+1-1)^2 + (-1)*1 = (-1)^2 - 1 = 0
б) a = 1; b = -1; N = (-1-1-1)^2 + (-1)*1 = (-3)^2 - 1 = 8
в) Или, например, ab = -1,5; ab + 2 = 0,5, тогда
a = 3; b = -0,5; N = (-0,5-3-1,5)^2 + (-1,5)*(0,5) = (-5)^2 - 0,75 = 24,25
г) Если, например, ab = -0,5; ab + 2 = 1,5, тогда
a = 0,5; b = -1; N = (-1-0,5-0,5)^2 + (-0,5)*(1,5) = (-2)^2 - 0,75 = 3,25
В любом случае, если произведение ab < 0 и ab + 2 > 0, то указанное выражение неотрицательно.
В пунктах 1) и 2) вычислили, что при ab >= 0 и при ab <= -2 выражение тоже неотрицательно.
Таким образом, мы доказали, что оно неотрицательно в любом случае.
Похожие вопросы
Предмет: Английский язык,
автор: Ser43627
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: shukurovas712
Предмет: Математика,
автор: aydan2002
Предмет: Математика,
автор: Аноним
и заметим что 2*(ab)*(a-b) очень похож на второй член квадрата суммы
(a-b)² = a² - 2ab + b²
(b-a)² + 2ab + 2ab(b-a) + a²b²+a²b² = (b-a)²+2ab(b-a)+a²b² + a²b²+2ab+1-1=(b-a+ab)²+(ab+1)²-1>=0