Предмет: Математика,
автор: Infinity167
найдите сумму целых решений неравенства
Приложения:
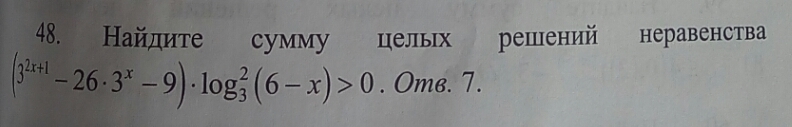
Ответы
Автор ответа:
2
Приложения:
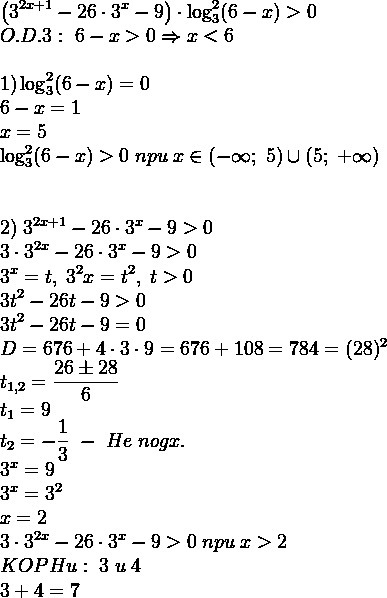
Похожие вопросы
Предмет: Оʻzbek tili,
автор: nasimovamexrangiz
Предмет: История,
автор: maksimshadr01933
Предмет: Математика,
автор: eskuzenovad
Предмет: Геометрия,
автор: morgunovanasta2