Предмет: Математика,
автор: Infinity167
найдите количество целых решений неравенства
Приложения:
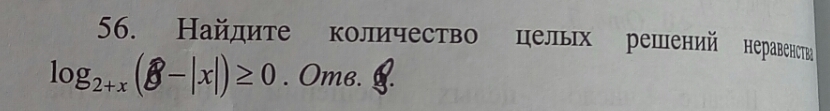
Ответы
Автор ответа:
1
Метод рационализации:
заменяем
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Обществознание,
автор: Аноним
Предмет: Математика,
автор: Ксюх7
Предмет: Литература,
автор: Аноним