Предмет: Математика,
автор: Клубничка2018
Помогите пожалуйста решить интеграл: dx/e^x+1?
Приложения:
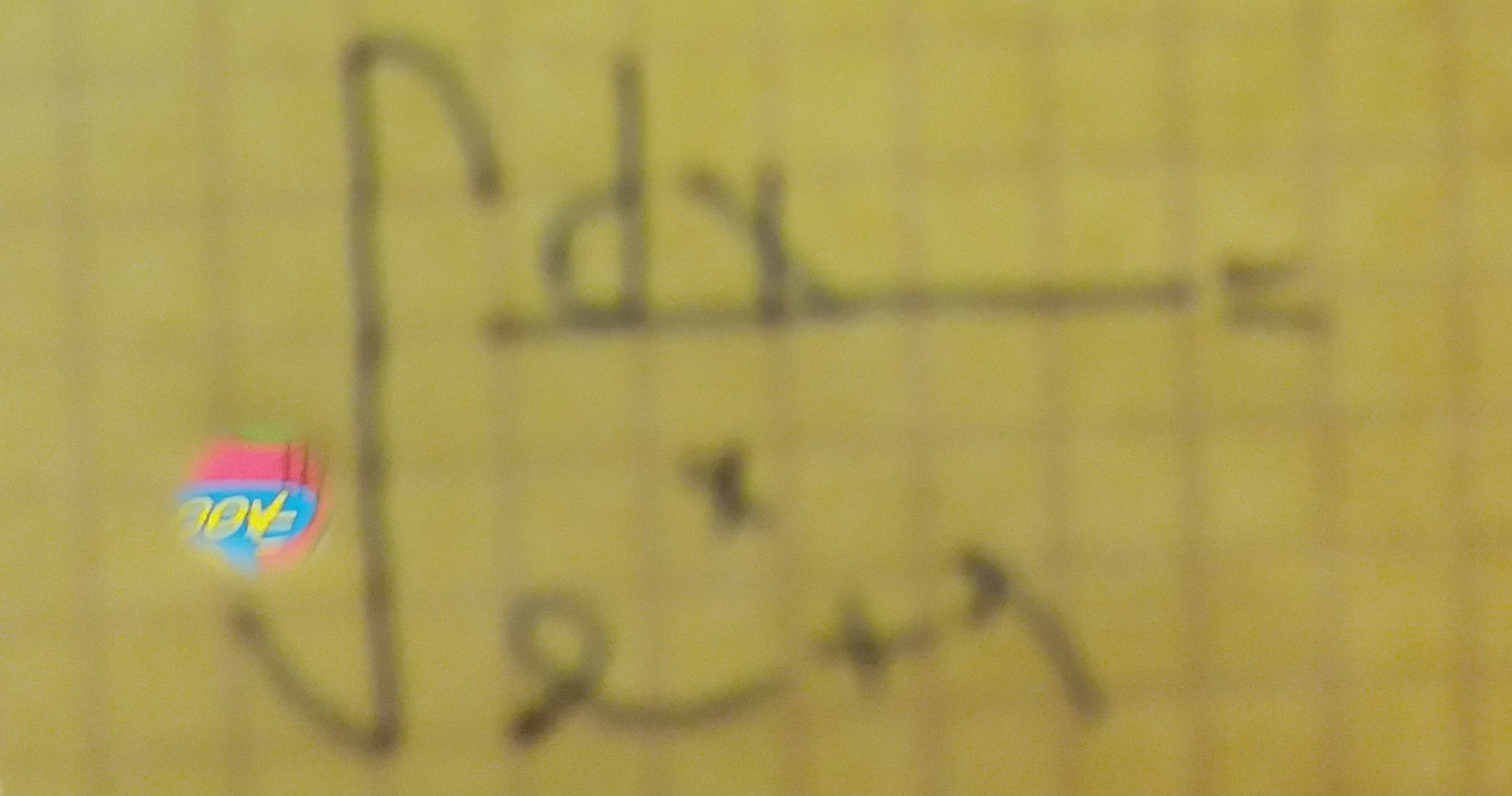
Ответы
Автор ответа:
1
Обозначим e^x=t⇒x=ln(t) и dx=dt/t. Тогда ∫dx/(e^x+1)=∫dt/[t*(t+1)]. Представим дробь 1/[t*(t+1)] в виде суммы дробей A/t+B/(t+1). Используя метод неопределённых коэффициентов, находим A=1, B=-1, так что 1/[t*(t+1)]=1/t-1/(t+1)]. Тогда ∫dt/[t*(t+1)]=∫dt/t-∫d(t+1)/(t+1)=ln/t/-ln/t+1/+ln(C)=ln[C*t/(t+1)], где C>0 - произвольная постоянная. Возвращаясь к переменной x, получаем ln[C*e^x/(e^x+1)]. Ответ: ln[C*e^x/(e^x+1)].
Похожие вопросы
Предмет: Английский язык,
автор: lan724674
Предмет: Английский язык,
автор: Аноним
Предмет: География,
автор: dashayurchenko2008
Предмет: Математика,
автор: настюшкахрюшка
Предмет: Биология,
автор: Schoolnik321