Предмет: Математика,
автор: настюша572
решение пределов по математике
Приложения:
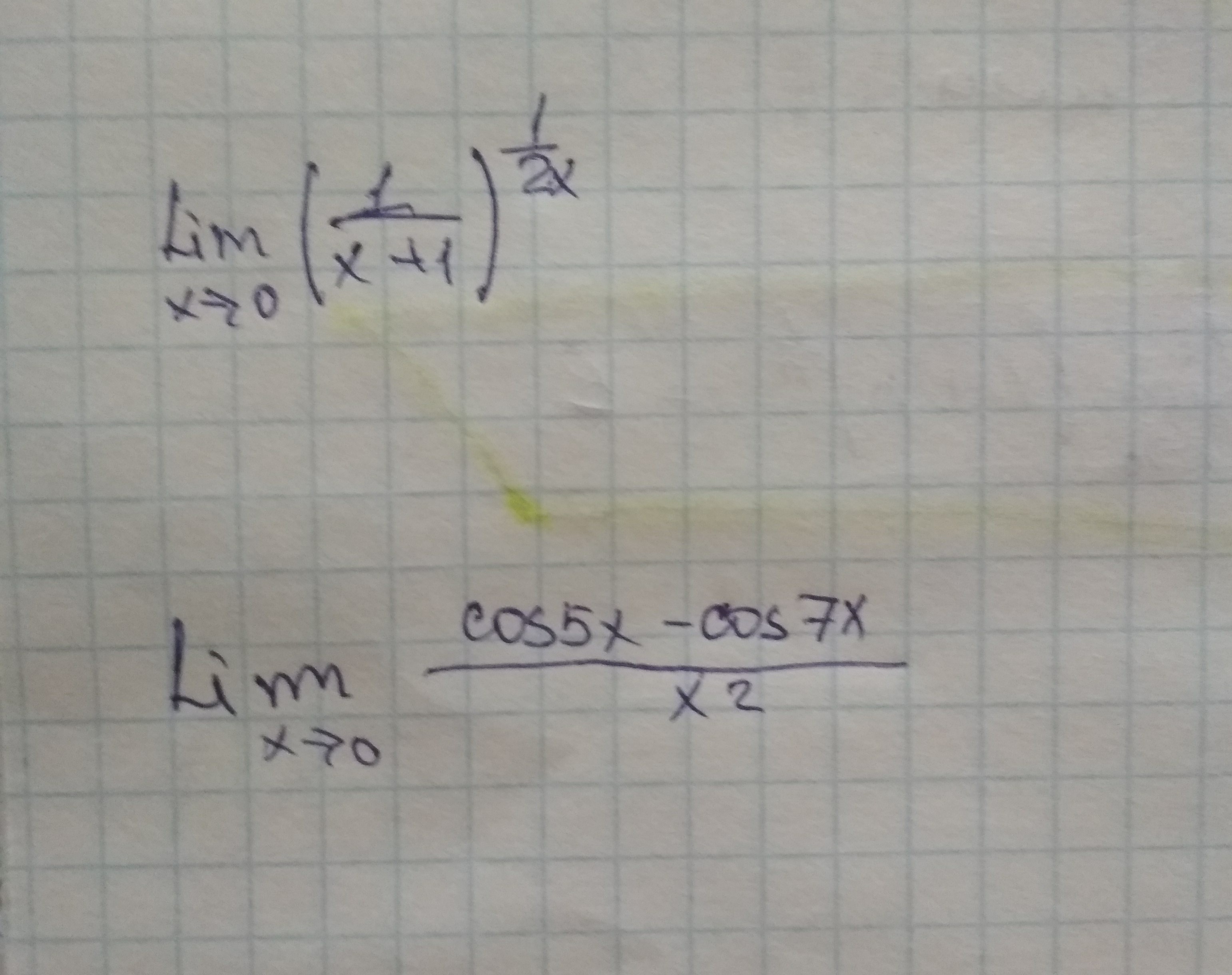
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: mishkafreddi30
Предмет: Физика,
автор: Odaodaoda
Предмет: Биология,
автор: Аноним
Предмет: Литература,
автор: videosolka