Предмет: Геометрия,
автор: JaikHit533
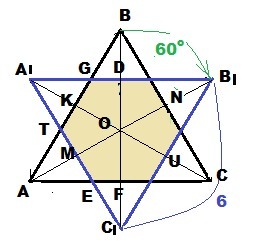
Правильный треугольник со стороной 6 повернули на угол 60° вокруг его центра. Найдите периметр шестиугольника, образовавшегося при пересечении этих треугольников.
Ответы
Автор ответа:
29
Центр треугольника ABC - пересечение медиан.
Медианы точкой пересечения делятся в отношении 2:1, считая от вершины ⇒ BO:OF = 2:1; AO:ON = 2:1; CO:OK = 2:1 ⇒
ΔABC повернули на 60° ⇒
ΔA₁B₁C₁: B₁O:OM = 2:1; A₁O:OU = 2:1; C₁O:OD = 2:1 ⇒
AM=MO=ON ⇒
ΔATM~ΔABN с коэффициентом подобия AN/AM = 3 ⇒
AT = TG = GB = 6/3 = 2 ⇒
Периметр полученного шестиугольника 2*6 = 12
Медианы точкой пересечения делятся в отношении 2:1, считая от вершины ⇒ BO:OF = 2:1; AO:ON = 2:1; CO:OK = 2:1 ⇒
ΔABC повернули на 60° ⇒
ΔA₁B₁C₁: B₁O:OM = 2:1; A₁O:OU = 2:1; C₁O:OD = 2:1 ⇒
AM=MO=ON ⇒
ΔATM~ΔABN с коэффициентом подобия AN/AM = 3 ⇒
AT = TG = GB = 6/3 = 2 ⇒
Периметр полученного шестиугольника 2*6 = 12
Приложения:
Похожие вопросы
Предмет: Математика,
автор: dzhonov001
Предмет: Химия,
автор: 7tz4qe8spj
Предмет: Қазақ тiлi,
автор: maya777777
Предмет: Алгебра,
автор: yuzeevmisha
Предмет: Алгебра,
автор: gajnullinaelwira