Question

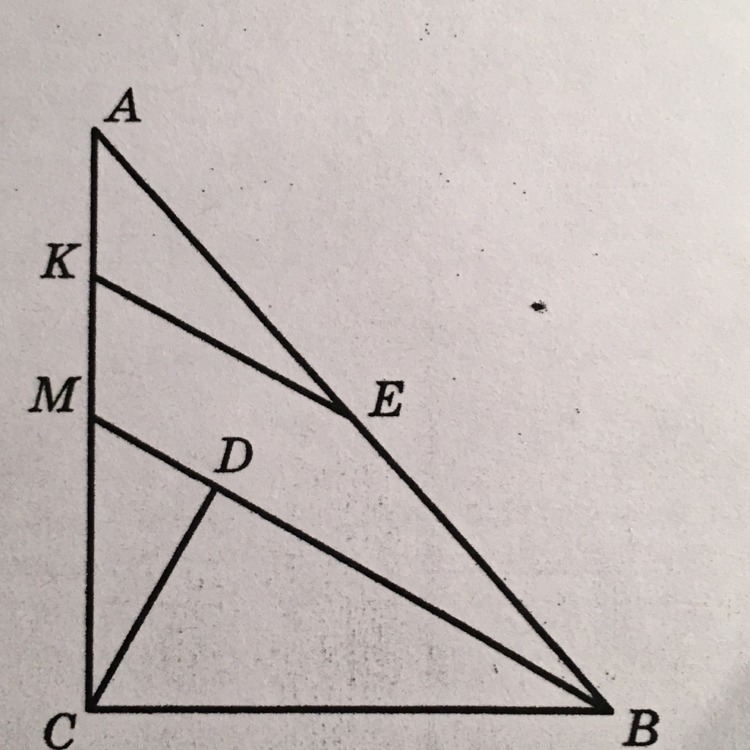
На рисунке 42 AC丄ВС, CD丄MB: Точки Е и К-середины отрезков АВ и АM, EK=12,5 см, DM-9 см. Найдите СМ и sin МВС

Answer 1

KE - средняя линия треугольника ΔAMB. Следовательно, MB = 2*EK = 2*12.5 = 25 см.
Треугольники ΔCMD и ΔCMB подобны по двум углам: ∠MCB = ∠MDC и ∠CMD = ∠CMB. Следовательно, MB : MC = MC : MD, или MC² = MB*MD
MC² = 25 * 9 = 225 и MC = 15 см.
∠MBC = ∠MCD.
Далее, синус равен отношению противолежащего угла к гипотенузе:
sin(∠MBC)= sin(∠MCD) = MD : MC = 9/25

Ответ:  15см и 9/25