Предмет: Математика,
автор: alievad101p4xwrd
СРОЧНО!!!! ПОМОГИТЕ ПОЖАЛУЙСТА!!!!
ЖЕЛАТЕЛЬНО РЕШИТЬ ВСЕ!!
Вариант 1
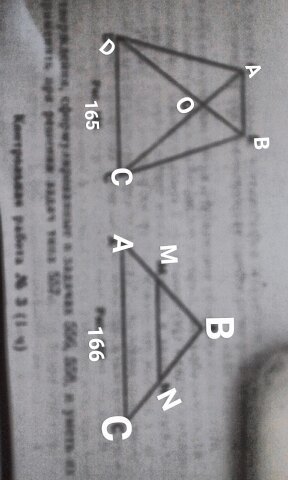
1. На рисунке 165 AB II CD. а) Докажите , что AO:OC=BO:OD. б) Найдите AB , если OD=15 см, OB=9 см, CD=25 см.
2. Найдите отношение площадей треугольников ABC и KMN , если AB=8 см, BC=12 см, AC=16 см, KM=10 см , MN=15 см, NK=20 см.
Вариант 2
1. На рисунке 166 MN II AC. а) Докажите, что AB*BN=CB*BM. б) Найдите MN, если AM=6 см, BM=8 см, AC=21 см.
2. Даны стороны треугольников PQR и ABC: PQ=16 см , QR=20 см, PR=28 см, AB=12 см, BC=15 см, AC=21 см. Найдите отношение площадей этих треугольников.
Приложения:
Ответы
Автор ответа:
6
1 вариант:
1)ΔАОВ подобен ΔСОD,т.к. угол AOB= углуCOD- так как вертикальные;
угол BAO= углу DCO и угол ABO= углу CDO - как накрестлежащие, тогда AO:OC=BO:OD (исходя из подобия треугольников)
2)ΔАВС подобен Δ KMN, тогда по коэффициенту подобия:
k = AB/KM = BC/MN = AC/NK = 8/10 но это число можно сократить, то есть k=8/10=4/5
Площади подобных фигур относятся,как квадрат коэффициента подобия:
S(ΔABC)/ S(ΔKMN) = k^2=(4/5)^2= 16/25
Отве:т 16/25
2 вариант:
1) ΔАВС подобен Δ MBN - по двум углам(угол В- общий, угол ВМN = углу ВАС- как соответственные при МN//АС и секущей АВ)
Треугольники подобны, значит сходственные стороны пропорциональны, то есть: АВ/ВМ=СВ/ВN, следовательно AB•BN = СВ•ВМ
АВ=АМ+МВ=6+8=14
МN/АС= ВМ/АВ; МN/21=8/14, МN=21·8/14=12
Ответ МN=12см
2) ΔPQR подобен ΔАВС (стороны их пропорциональны):
k=PQ/AB=QR/BC=PR/AC=16/12=20/15=28/21, значит k=4/3
S(ΔPQR)/ S(ΔАВС) = k^2=(4/3)²=16/9
Отве:т 16/9
1)ΔАОВ подобен ΔСОD,т.к. угол AOB= углуCOD- так как вертикальные;
угол BAO= углу DCO и угол ABO= углу CDO - как накрестлежащие, тогда AO:OC=BO:OD (исходя из подобия треугольников)
2)ΔАВС подобен Δ KMN, тогда по коэффициенту подобия:
k = AB/KM = BC/MN = AC/NK = 8/10 но это число можно сократить, то есть k=8/10=4/5
Площади подобных фигур относятся,как квадрат коэффициента подобия:
S(ΔABC)/ S(ΔKMN) = k^2=(4/5)^2= 16/25
Отве:т 16/25
2 вариант:
1) ΔАВС подобен Δ MBN - по двум углам(угол В- общий, угол ВМN = углу ВАС- как соответственные при МN//АС и секущей АВ)
Треугольники подобны, значит сходственные стороны пропорциональны, то есть: АВ/ВМ=СВ/ВN, следовательно AB•BN = СВ•ВМ
АВ=АМ+МВ=6+8=14
МN/АС= ВМ/АВ; МN/21=8/14, МN=21·8/14=12
Ответ МN=12см
2) ΔPQR подобен ΔАВС (стороны их пропорциональны):
k=PQ/AB=QR/BC=PR/AC=16/12=20/15=28/21, значит k=4/3
S(ΔPQR)/ S(ΔАВС) = k^2=(4/3)²=16/9
Отве:т 16/9
Похожие вопросы
Предмет: Английский язык,
автор: botbot1559
Предмет: Химия,
автор: lashkis52
Предмет: Математика,
автор: denisdzabaev38
Предмет: Математика,
автор: yushukina2016
Предмет: Обществознание,
автор: mdron1