Предмет: Геометрия,
автор: Madam362
ПОМОГИТЕ ЗАДАЧИ ПРОСТЫЕ, НО ЗАТРУДНЯЮСЬ В ЭТИХ ЗАДАЧАХ!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:


Madam362:
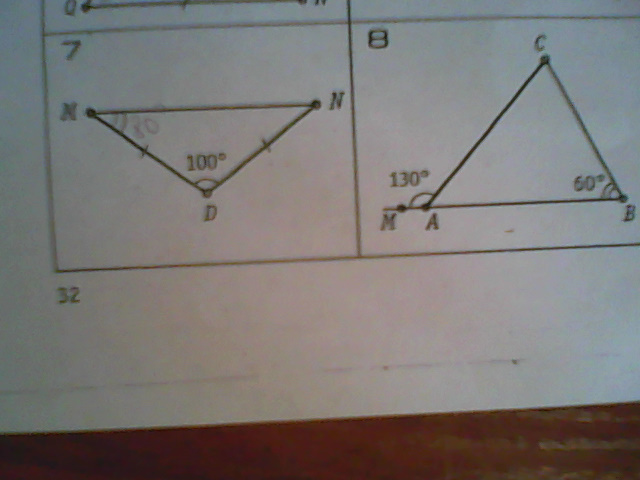
Нужно найти все неизвестные углы
Рисунок 7, там не 80 градусов. а чтото другое. Т.к. на угол N тогда остаеться 0 градусов.
Ответы
Автор ответа:
2
7. Если угол M=80, а стороны MD=ND, то N=80, так как треугольник равнобедренный
8. Внешний угол треугольника равен сумме двух других углов, не смежных с ним, значит, C= 130-60=70, MAC=180-(60+70)=50(сумма всех углов треугольника равна 180)
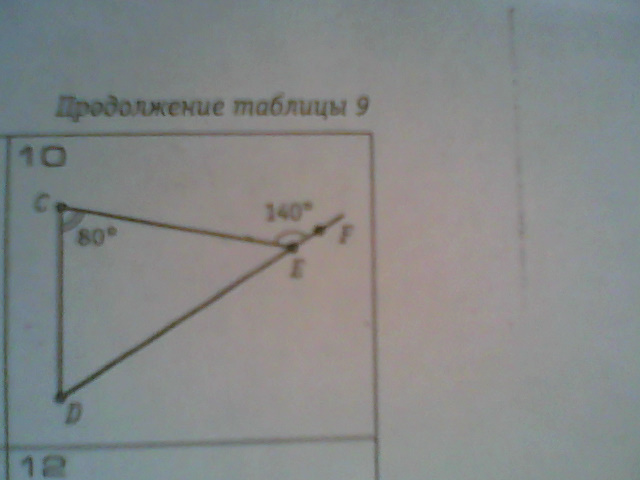
10. Теорема такая же, как и в 8. D=140-80=60, DEC=180-(60+80)=40
8. Внешний угол треугольника равен сумме двух других углов, не смежных с ним, значит, C= 130-60=70, MAC=180-(60+70)=50(сумма всех углов треугольника равна 180)
10. Теорема такая же, как и в 8. D=140-80=60, DEC=180-(60+80)=40
Автор ответа:
2
#7
Если треугольник MND - равнобедренный, то углы при основании равны. Тогда
<MND=<NMD=(180-100):2=40°
Ответ: 40;40.
#8
Если угол MAC- внешний, то он равен сумме двух углов треугольника с ним не смежным.
Значит
<С=130°-60°=70°
Так как сумма углов в треугольнике равна 180° , то
<A=180°-(60°+70°)=50°
Ответ:70;50.
#10
Если угол СЕF- внешний, то он равен сумме двух углов треугольника с ним не смежным.
Из этого следует, что
<C+<D=140°
Если <С=80°, то
<D=140°-80°=60°
Тогда, если сумма углов в треугольнике равна 180°, то можно найти <CED=180°-140°=40°
Ответ:60;40
Если треугольник MND - равнобедренный, то углы при основании равны. Тогда
<MND=<NMD=(180-100):2=40°
Ответ: 40;40.
#8
Если угол MAC- внешний, то он равен сумме двух углов треугольника с ним не смежным.
Значит
<С=130°-60°=70°
Так как сумма углов в треугольнике равна 180° , то
<A=180°-(60°+70°)=50°
Ответ:70;50.
#10
Если угол СЕF- внешний, то он равен сумме двух углов треугольника с ним не смежным.
Из этого следует, что
<C+<D=140°
Если <С=80°, то
<D=140°-80°=60°
Тогда, если сумма углов в треугольнике равна 180°, то можно найти <CED=180°-140°=40°
Ответ:60;40
Спасибо большое, обращайся ещё
Похожие вопросы
Предмет: Русский язык,
автор: akylaimoldokulova
Предмет: Английский язык,
автор: daniardaulet2005
Предмет: Английский язык,
автор: zargalsansuev
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Аноним