Предмет: Математика,
автор: Neznakomiy2289
Номер 9 : О) П) Р) С)
Приложения:
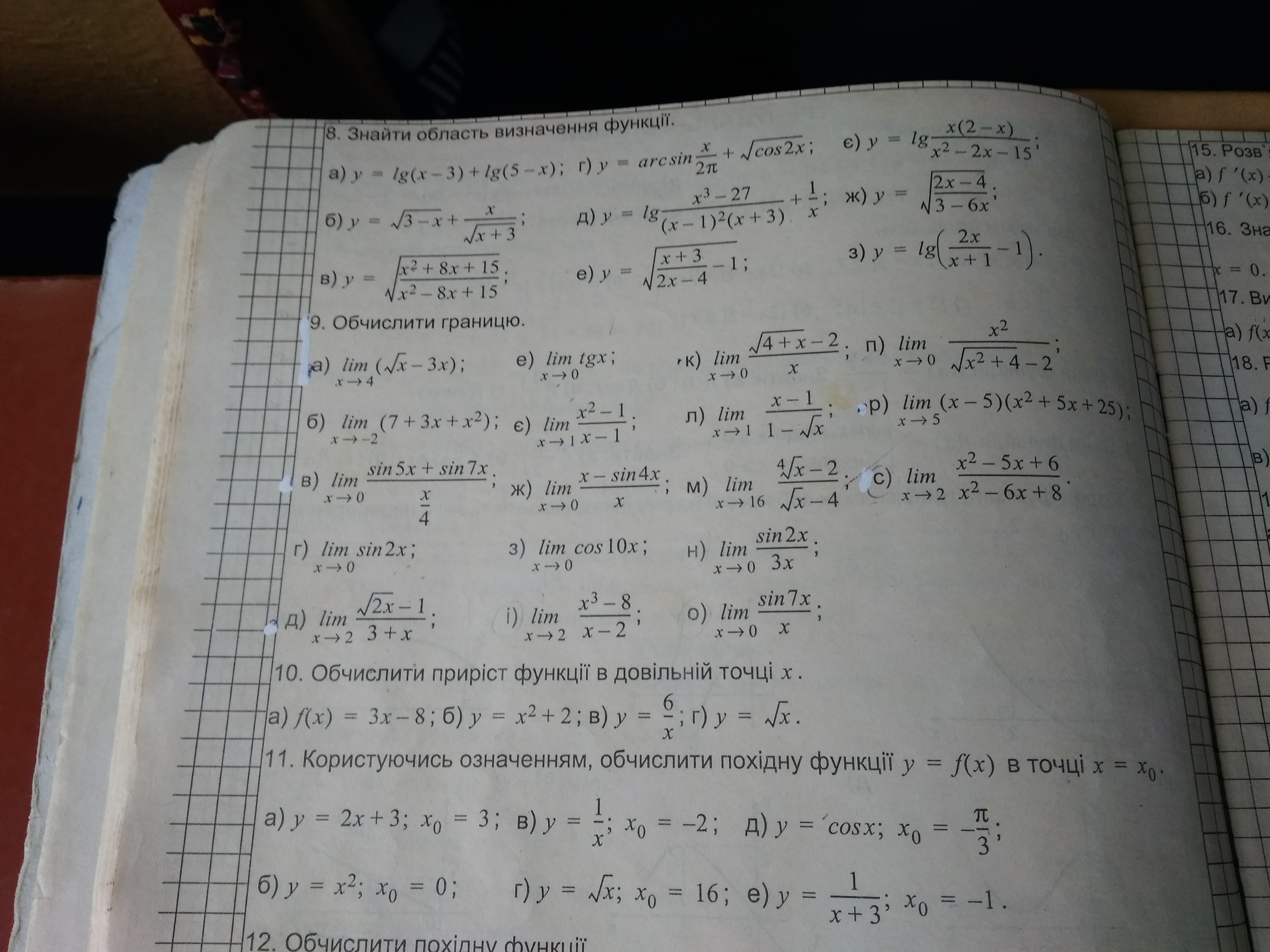
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: salahielvira
Предмет: Математика,
автор: pubgmobile2344h
Предмет: Математика,
автор: minjanajzere
Предмет: Литература,
автор: 66674
Предмет: Биология,
автор: катюшаюля