Предмет: Математика,
автор: Den974
Помогите пожалуйста.
Решить дифференциальное уравнение
Приложения:
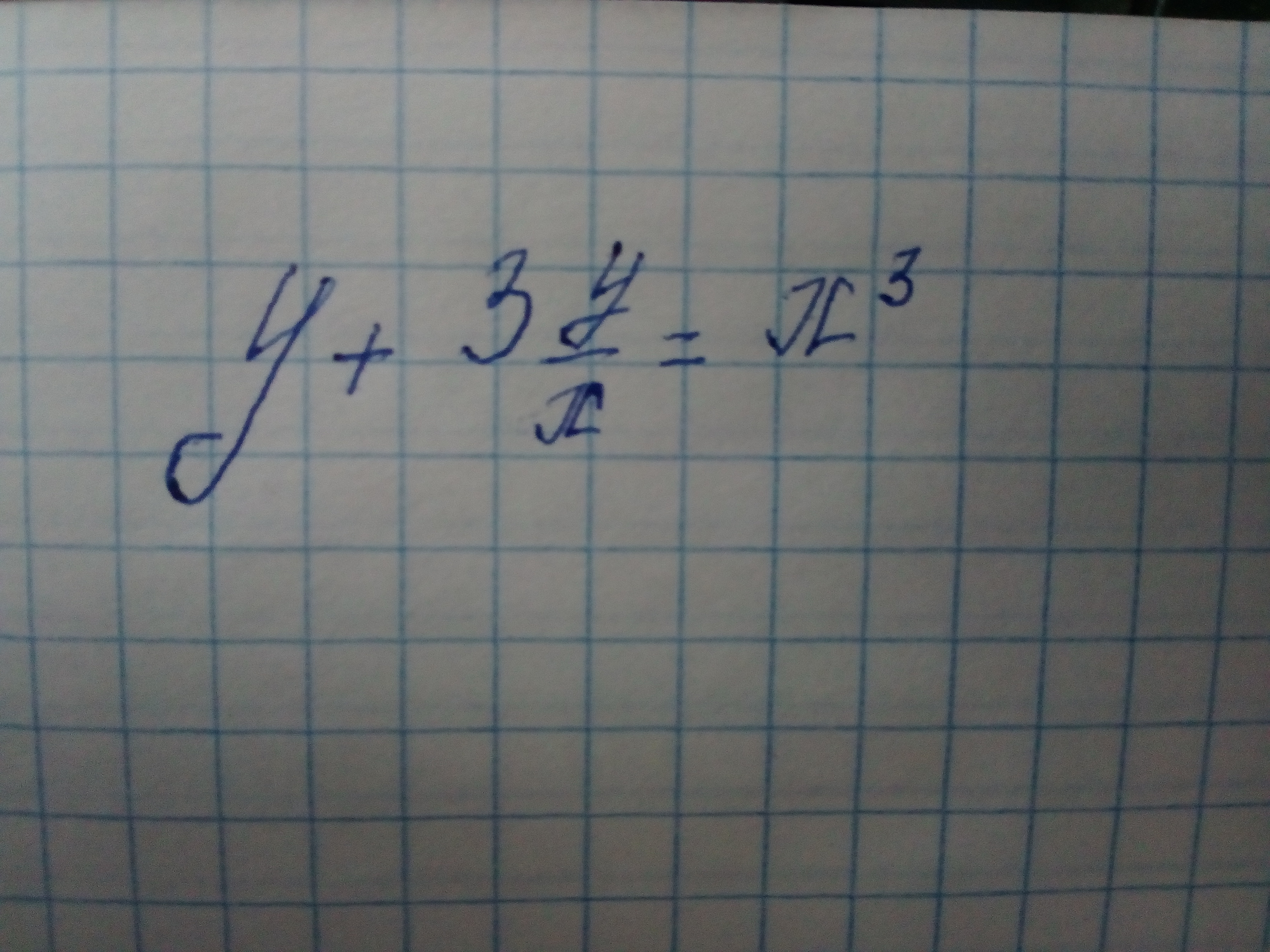
Ответы
Автор ответа:
2
Полагаю, в задании описка: первый y должен быть со штрихом.

Выполняем замену:

Подставляем в исходное уравнение:

Разбиваем на систему уравнений:

u и v найдены, выполним обратную замену y=uv:

Выполняем замену:
Подставляем в исходное уравнение:
Разбиваем на систему уравнений:
u и v найдены, выполним обратную замену y=uv:
Похожие вопросы
Предмет: Химия,
автор: podtvoejkrovatumonst
Предмет: Математика,
автор: SASHANENARKOMAN
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Albinaabeka
Предмет: Математика,
автор: ольга338