Предмет: Математика,
автор: lecilors
Дана функция y=2-x^(2)
Найти производную y'
Поставить в производную x0 = -3
Поставить в функцию x0 = -3
Составить уравнение касательной к графику данной функции в точке с абсциссой x0
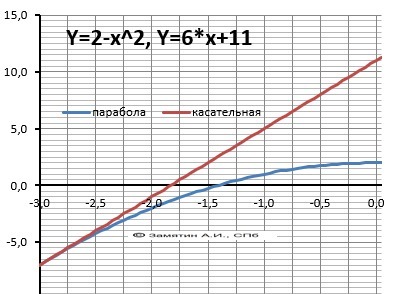
Выполнить рисунок
Вычислить площадь треугольника, ограниченного отрезками касательной и осей координат.
Ответы
Автор ответа:
1
ДАНО
Y = - x² + 2
Xo = -3
НАЙТИ
Уравнение касательной.
Площадь под касательной.
РЕШЕНИЕ
Уравнение касательной:
Y = Y'(Xo)*(x-Xo) + Y(Xo)
Производная функции.
Y'(x) = - 2*x.
Y'(-3) = 6, Y(-3) = -7
Уравнение касательной в точке Хо = -3
Y = 6*x + 11,
Находим площадь треугольника.
а = У(0) = 11 - пересечение с осью У.
b = - 11/6 - пересечение с осью Х.
Площадь по формуле
S = a*|b|/2 = 11* 11/6 : 2 =121/12 = 10 1/12 - площадь - ОТВЕТ
Рисунок к задаче в приложении.
Y = - x² + 2
Xo = -3
НАЙТИ
Уравнение касательной.
Площадь под касательной.
РЕШЕНИЕ
Уравнение касательной:
Y = Y'(Xo)*(x-Xo) + Y(Xo)
Производная функции.
Y'(x) = - 2*x.
Y'(-3) = 6, Y(-3) = -7
Уравнение касательной в точке Хо = -3
Y = 6*x + 11,
Находим площадь треугольника.
а = У(0) = 11 - пересечение с осью У.
b = - 11/6 - пересечение с осью Х.
Площадь по формуле
S = a*|b|/2 = 11* 11/6 : 2 =121/12 = 10 1/12 - площадь - ОТВЕТ
Рисунок к задаче в приложении.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: josspeen
Предмет: Русский язык,
автор: meow222882828
Предмет: Русский язык,
автор: mapikmakar
Предмет: Математика,
автор: Zorro101
Предмет: Алгебра,
автор: sadovnikova