Предмет: Алгебра,
автор: luttelurium
6,7,8, пожалуйста!
Буду очень благодарна, + балы
Приложения:

Ответы
Автор ответа:
1
!!!!!!!!!!!!!!!!!!!!!
Приложения:

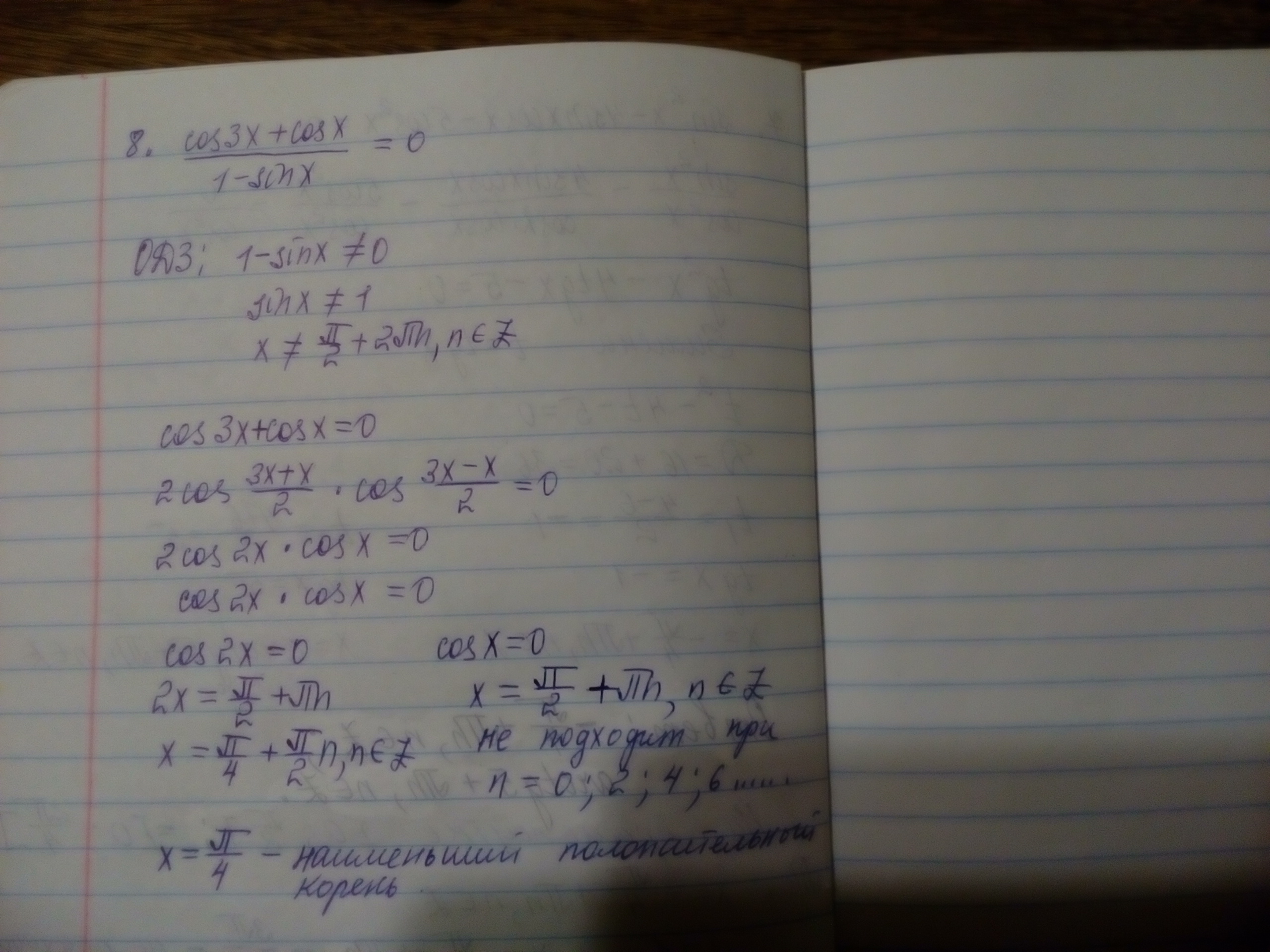
luttelurium:
Спасибо! Вы святой человек, не знаю, что бы делала без вас!
Автор ответа:
0
3 хз, сорри, во втором у меня сомнения проверь у кого-нибудь если можешь
Похожие вопросы
Предмет: Другие предметы,
автор: kretinina16102020
Предмет: Алгебра,
автор: vadimromanenko07
Предмет: Английский язык,
автор: lol22833
Предмет: Математика,
автор: igor87357petrov