Предмет: Математика,
автор: bratushko1039
Найти Область сходимости степенного ряда
Приложения:
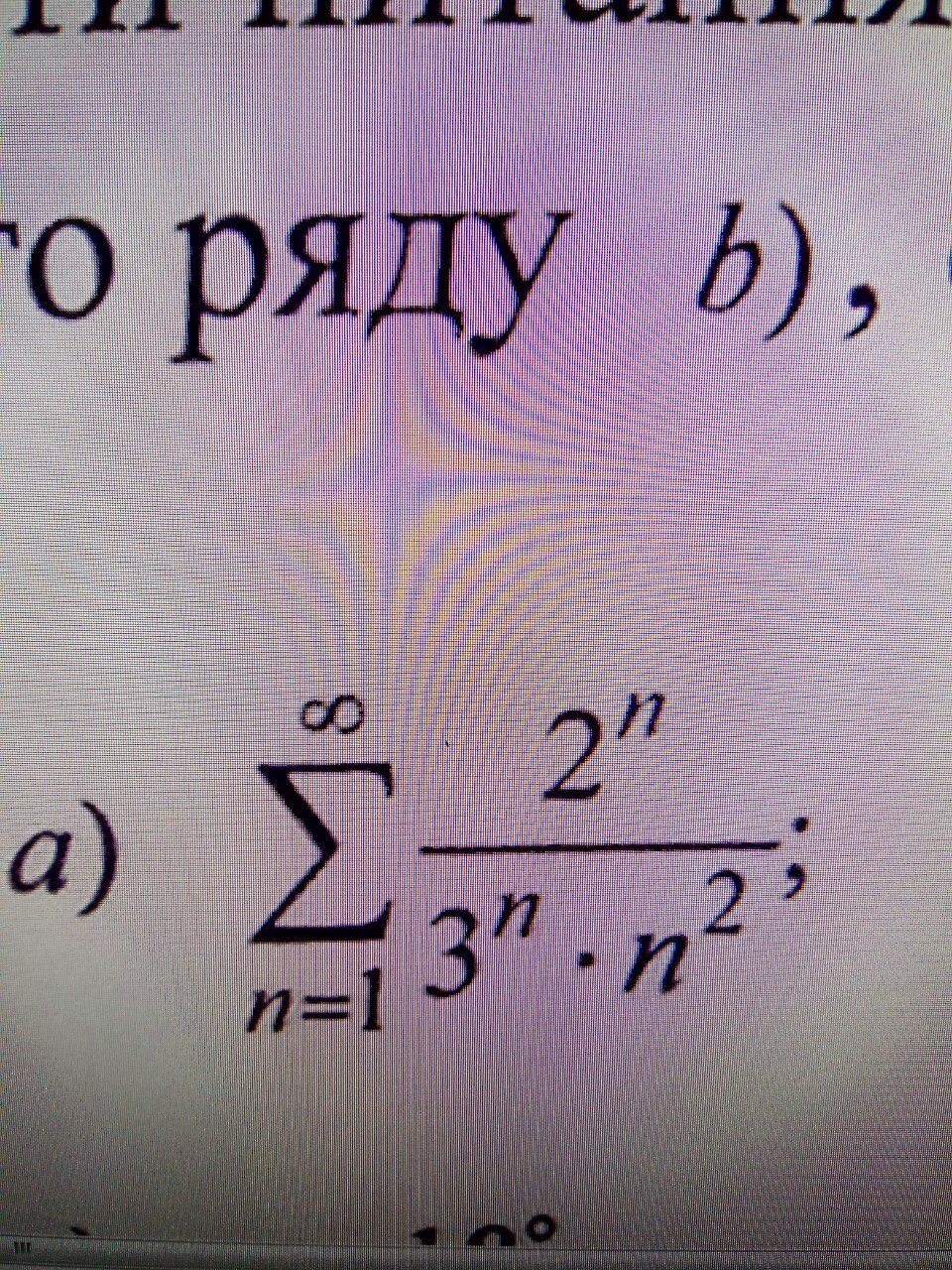
Vasily1975:
Здесь отсутствует переменная, поэтому это не степенной, а числовой ряд.
Поэтому я решу задачу, но отмечаю нарушение.
Ответы
Автор ответа:
0
Сравним данный числовой ряд с рядом обратных квадратов ∑1/n². Так как 2ⁿ/3ⁿ=(2/3)ⁿ<1, то члены данного ряда меньше соответствующих членов ряда обратных квадратов, т.е. 2ⁿ/(3ⁿ*n²)<1/n². А так как ряд обратных квадратов сходится, то, используя признак сравнения рядов, заключаем, что сходится и данный ряд. Ответ: ряд сходится.
Задача решена - ряд сходится. Но об области сходимости речь идти не может, так как для числовых рядов такого понятия не существует.
Я не знаю. У меня стоит именно такое условие
Условие неправильное. Область сходимости существует для функционального ряда, но не для числового.
А функциональный ряд - это ряд, члены которого являются не числа, а функции - одной или нескольких переменных. В данном же случае членами ряда являются числа, потому и ряд -числовой.
Спасбо
Похожие вопросы
Предмет: Геометрия,
автор: OshimaTakuboku
Предмет: Математика,
автор: jejejdjdnsjshdj
Предмет: История,
автор: YoZhukYT
Предмет: Математика,
автор: почемуха1
Предмет: Математика,
автор: daryaivanova205