Question

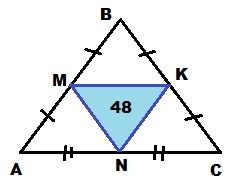
Длины сторон треугольника относятся как 5:6:5. Соединив середины его сторон, получили треугольник площадью 48. Тогда чему равен периметр исходного треугольника?

Answer 1

ΔABC:  AM=MB; BK=KC; AN=NC  ⇒  MK,KN,MN  - средние линии ⇒
AC = 2MK; AB = 2NK; BC = 2MN  ⇒  
ΔABC ~ ΔKNM по трем пропорциональным сторонам с коэффициентом подобия k=2   ⇒  
Периметр ΔABC в два раза больше периметра  ΔKNM

По условию AB:AC:BC = 5:6:5   ⇒   NK:MK:MN = 5:6:5   ⇒
NK = 5x; MK=6x; MN=5x; 
$P_{KNM}$=5x+6x+5x = 16x;    p= $\frac{P_{KNM}}{2}$ = 16x/2 = 8x
Площадь ΔKNM по формуле Герона
$S_{KNM}= \sqrt{p(p-a)(p-b)(p-c)} =48 \\ \\ \sqrt{8x(8x-5x)(8x-6x)(8x-5x)} =48 \\ \\ \sqrt{8x*3x*2x*3x} =48$
$\sqrt{144x^4} =48$
 12x²=48   ⇒    x²=4    ⇒   x=2
$P_{KNM}=16x=16*2=32$
$P_{ABC}=k*P_{KNM}=2*32=64$

Ответ: периметр исходного треугольника равен 64