Question

Помогите с математикой
1)Прямоугольник большая сторона которого равна 4 мм , диагональ равна 5 мм , вращается вокруг меньшей стороны. Найдите площадь поверхности получившегося тела вращения.
2)Прямоугольный треугольник с катетами 8 дм и 15 дм вращается вокруг большего катета. Найдите площадь полной поверхности получившегося тела вращения.
Желательно с рисунком и чтобы было дано
Заранее спасибо)

Answer 1

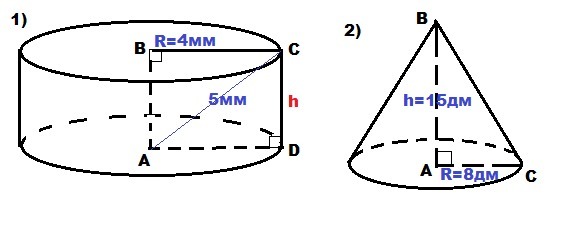
1. Дано: прямоугольник ABCD; AD=BC = 4 мм; AC = 5 мм

   В результате вращения прямоугольника получится цилиндр.
   Радиус основания равен большей стороне прямоугольника
   R = BC = 4мм.  
   Высоту цилиндра можно найти из прямоугольного треугольника ACD по теореме Пифагора
   h² = AC² - AD² = 5² - 4² = 9    ⇒     h = √9 = 3 мм

Площадь поверхности цилиндра равна сумме площадей боковой поверхности и двух оснований.
S₆ = 2πRh = 2π*4*3 = 24π мм²
S₀ = πR² = π*4² = 16π мм²
S = S₆ + 2S₀ = 24π + 2*16π = 56π мм²

2. Дано: ΔABC:  ∠A=90°;  AB=15 дм; AC=8 дм; 

AB - ось вращения треугольника.
В результате вращения образуется конус: R = AC = 8 дм
Образующая конуса равна гипотенузе  BC. Теорема Пифагора
BC² = AB² + AC² = 15² + 8² = 225 + 64 = 289
BC = √289 = 17 дм

Площадь полной поверхности конуса равна сумме площади боковой поверхности и площади основания
S₆ = πR*BC = π*8*17 = 136π дм²
S₀ = πR² = π*8² = 64π дм²
S = S₆ + S₀ = 136π + 64π = 200π дм²