Предмет: Алгебра,
автор: Nejdan1
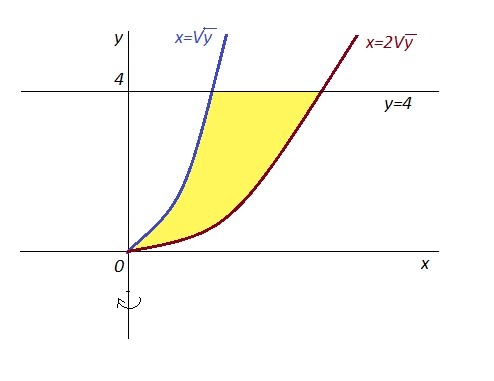
Найти обьём тела, полученного вращением вокруг оси Oy фигуры, ограниченной линиями x=y^(1/2); x=2*y^(1/2); y=4
Ответы
Автор ответа:
1
x=√y и x=2√y - это правые ветви парабол y=x² и y=x²/4 .

Приложения:
Nejdan1:
Премного благодарен)
Похожие вопросы
Предмет: Русский язык,
автор: Solovevaolga12273
Предмет: Математика,
автор: karinchik95
Предмет: Алгебра,
автор: doxf374
Предмет: Математика,
автор: katuha29529like