Предмет: Геометрия,
автор: Alisa11221122
докажите, что сумма медиан треугольника меньше его периметра! помогите пожалуйста)
Ответы
Автор ответа:
16
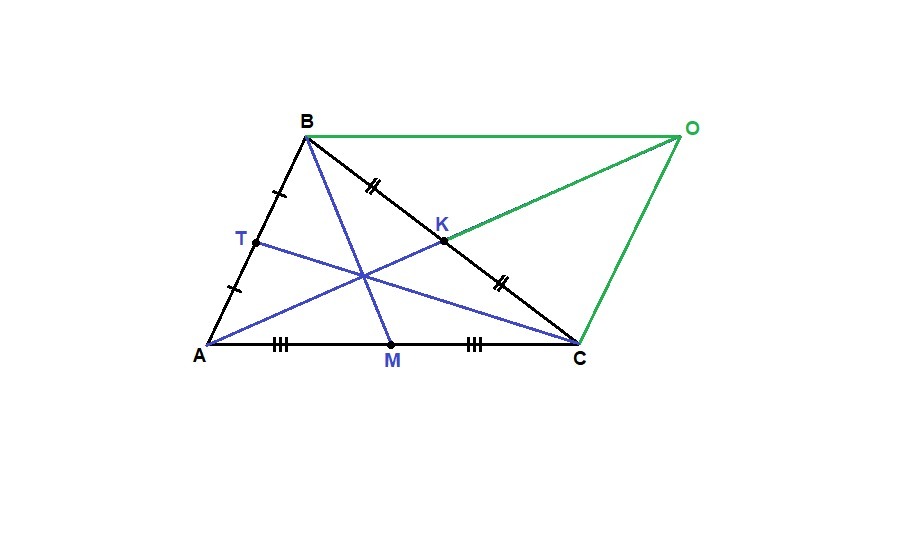
АК, ВМ и СТ - медианы треугольника АВС.
Надо доказать, что АК + ВМ + СТ < АВ + ВС + АС.
Отложим на луче АК отрезок КО = АК.
КО = АК по построению, ВК = КС, так как АК медиана.
Если в четырехугольнике диагонали точкой пересечения делятся пополам, то это параллелограмм.
Значит АВОС - параллелограмм. Тогда ВО = АС.
Каждая сторона треугольника меньше суммы двух других сторон, значит в треугольнике АВО: АО < AB + BO, а значит и 2АК < АВ + АС, т.е.
АК < 1/2 (АВ + АС)
Аналогично, построив параллелограммы с диагоналями, содержащими две другие медианы, докажем , что
ВМ < 1/2 (ВА + ВС) и
СТ < 1/2 (СА + СВ)
Сложим эти три неравенства:
АК + ВМ + СТ < 1/2 АВ + 1/2 АС + 1/2 ВА + 1/2 ВС + 1/2 СА + 1/2 СВ
АК + ВМ + СТ < АВ + АС + ВС
АК + ВМ + СТ < Рabc
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: serebryanskaya24
Предмет: Математика,
автор: bushenkoma
Предмет: Математика,
автор: Ktoto228povar
Предмет: Математика,
автор: униса
Предмет: Алгебра,
автор: myachin667