Предмет: Математика,
автор: rubrand
Помогите пожалуйста. Очень срочно
Приложения:
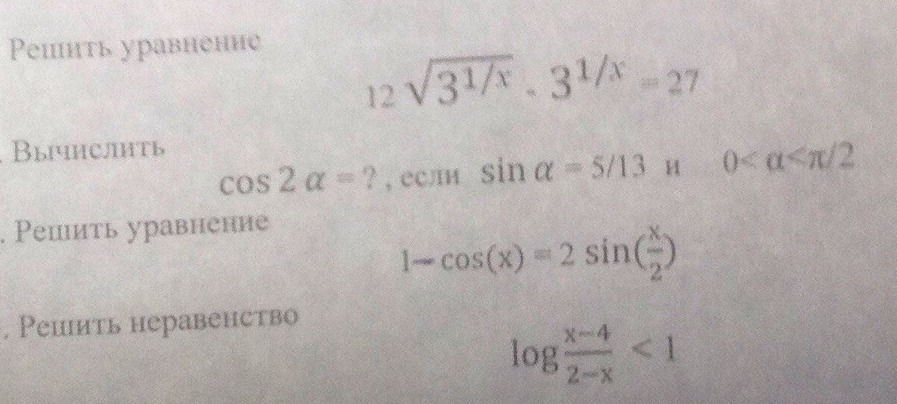
Аноним:
у логарифма какое основание?
Все что было, ничего больше не знаю. Ничего не говорят
без основания неравенство не решить...
мб что то другое. очень мало времени осталось
Ответы
Автор ответа:
1
1) √3^1/x = t
12t - t² = 27
t² -12t +27 = 0
по т. Виета корни 3 и 9
а)t = 3
√3^1/x = t
√3^1/x = 3
1/(2х) = 1
2х = 1
х = 1/2
б) √3^1/x = t
√3^1/x = 9
1/(2х) = 9
2х = 1/9
х = 1/18
2) Cos2α = 1 - 2Sin²α = 1 - 2*25/169 = 1 - 50/169= 119/169
Сos2α =√119/13
3) 1 - Сosx = 2Sinx/2
Sin²x/2 + Сos²x/2 - Cos²x/2 +Sin²x/2 = 2Sinx/2
Sin²x/2 -Sinx/2 = 0
Sinx/2(Sinx/2 -1) = 0
Sinx/2 = 0 или Sinx/2 -1 = 0
x/2 = nπ, n ∈Z Sinx/2 = 1
x = 2πn , n ∈Z x/2 = π/2 + 2πk , k ∈Z
x = π +4πk , k ∈Z
12t - t² = 27
t² -12t +27 = 0
по т. Виета корни 3 и 9
а)t = 3
√3^1/x = t
√3^1/x = 3
1/(2х) = 1
2х = 1
х = 1/2
б) √3^1/x = t
√3^1/x = 9
1/(2х) = 9
2х = 1/9
х = 1/18
2) Cos2α = 1 - 2Sin²α = 1 - 2*25/169 = 1 - 50/169= 119/169
Сos2α =√119/13
3) 1 - Сosx = 2Sinx/2
Sin²x/2 + Сos²x/2 - Cos²x/2 +Sin²x/2 = 2Sinx/2
Sin²x/2 -Sinx/2 = 0
Sinx/2(Sinx/2 -1) = 0
Sinx/2 = 0 или Sinx/2 -1 = 0
x/2 = nπ, n ∈Z Sinx/2 = 1
x = 2πn , n ∈Z x/2 = π/2 + 2πk , k ∈Z
x = π +4πk , k ∈Z
Спасибо большое
;)
Похожие вопросы
Предмет: Математика,
автор: kiriiilllll10
Предмет: Геометрия,
автор: logockayazvezda
Предмет: Математика,
автор: kiriiilllll10
Предмет: Математика,
автор: zulya2004
Предмет: Алгебра,
автор: Ивангай11